AI tutor
Full solution
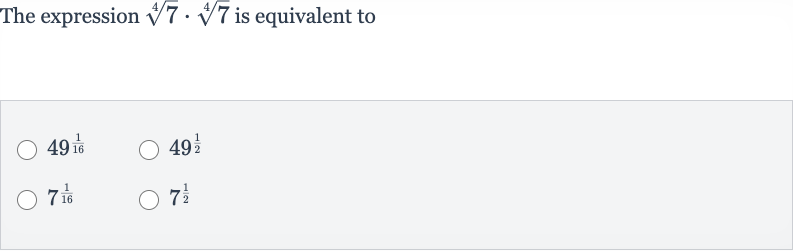
Q. The expression is equivalent to
- Understand the problem: Understand the problem. We need to find the equivalent expression for the product of two fourth roots of .
- Use property of exponents: Use the property of exponents for roots.The fourth root of a number can be written as that number raised to the power. So, can be written as .
- Multiply the expressions: Multiply the expressions.We have . When multiplying expressions with the same base, we add the exponents.
- Add the exponents: Add the exponents.
- Simplify the exponent: Simplify the exponent. simplifies to , because reduces to .
- Write the final answer: Write the final answer.The equivalent expression for is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help