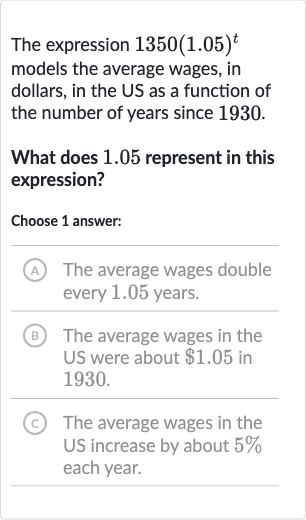
The expression 1350(1.05)^(t) models the average wages, in dollars, in the US as a function of the number of years since 1930 . What does 1.05 represent in this expression? Choose 1 answer: (A) The average wages double every 1.05 years. (B) The average wages in the US were about $1.05 in 1930. (C) The average wages in the US increase by about 5% each year.

Question

The expression  1350(1.05)^(t) models the average wages, in dollars, in the US as a function of the number of years since 1930 . What does 1.05 represent in this expression? Choose 1 answer: (A) The average wages double every 1.05 years. (B) The average wages in the US were about  $1.05 in 1930. (C) The average wages in the US increase by about  5% each year.

Bytelearn · Accepted Answer

Structure of Expression: The expression given is 1350(1.05)^(t), which models the average wages in the US as a function of time since 1930. To understand what 1.05 represents, we need to look at the structure of the expression. It is an exponential function where 1.05 is the base raised to the power of t, which represents time in years. In the context of growth, the base of an exponential function (greater than 1) indicates the growth factor per unit of time.Interpretation of Base: Since the base is 1.05, this suggests that for each year (t), the average wages are multiplied by 1.05. This multiplication by 1.05 is equivalent to a 5% increase each year because 1.05 is 100% of the previous year's wages plus an additional 5%.Evaluation of Choices: Now, let's evaluate the choices given: (A) The average wages double every 1.05 years. - This is incorrect because the expression does not imply doubling; it implies a steady growth rate. (B) The average wages in the US were about $1.05 in 1930. - This is incorrect because the 1350 in the expression likely represents the initial average wages in 1930, not 1.05. (C) The average wages in the US increase by about 5% each year. - This is correct because the base of the exponential function, 1.05, indicates a 5% increase.

Full solution

More problems from Interpreting Linear Expressions

Related topics