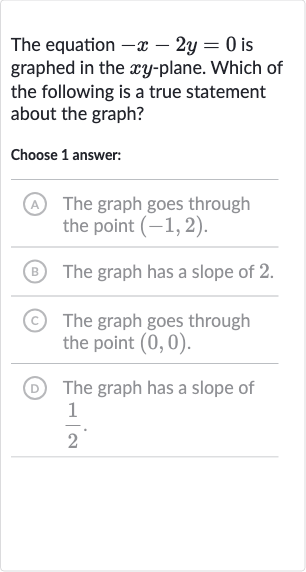
The equation $\newline$ $-x-2y=0$ is graphed in the $\newline$ $xy$ -plane. Which of the following is a true statement about the graph? $\newline$ Choose $1$ answer: $\newline$ (A) The graph goes through the point $\newline$ $(-1,2)$ . $\newline$ (B) The graph has a slope of $2$ . $\newline$ (C) The graph goes through the point $\newline$ $(0,0)$ . $\newline$ (D) The graph has a slope of $\newline$ $\frac{1}{2}$ .

Full solution

Q. The equation

\newline

-x-2y=0

is graphed in the

\newline

xy

-plane. Which of the following is a true statement about the graph?

\newline

Choose

1

answer:

\newline

(A) The graph goes through the point

\newline

(-1,2)

\newline

(B) The graph has a slope of

2

\newline

\newline

(0,0)

\newline

(D) The graph has a slope of

\newline

\frac{1}{2}

Rewrite Equation: Rewrite the equation in slope-intercept form to find the slope and y-intercept. $\newline$ The equation given is $-x - 2y = 0$ . To rewrite it in slope-intercept form $(y = mx + b)$ , we need to solve for $y$ . $\newline$ Add $x$ to both sides to get $-2y = x$ . $\newline$ Now divide both sides by $-2$ to isolate $y$ : $y = (-\frac{1}{2})x$ .
Analyze Slope-Intercept Form: Analyze the slope-intercept form to determine the slope and y-intercept. $\newline$ From the equation $y = (-\frac{1}{2})x$ , we can see that the slope ( $m$ ) is $-\frac{1}{2}$ and the y-intercept ( $b$ ) is $0$ , which means the graph goes through the origin $(0,0)$ .
Check Given Points: Check the given points and slopes against the slope-intercept form. $\newline$ (A) The graph goes through the point $(-1,2)$ . To check this, substitute $x = -1$ and $y = 2$ into the equation $y = (-1/2)x$ . We get $2 = (-1/2)(-1) = 1/2$ , which is not true. So, option (A) is incorrect. $\newline$ (B) The graph has a slope of $2$ . This is not true because we found the slope to be $-1/2$ . So, option (B) is incorrect. $\newline$ (C) The graph goes through the point $(0,0)$ . This is true because the y-intercept is $0$ , which means the graph goes through the origin. So, option (C) is correct. $\newline$ (D) The graph has a slope of $(1)/(2)$ . This is not true because we found the slope to be $-1/2$ , not $x = -1$ $1$ . So, option (D) is incorrect.