Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

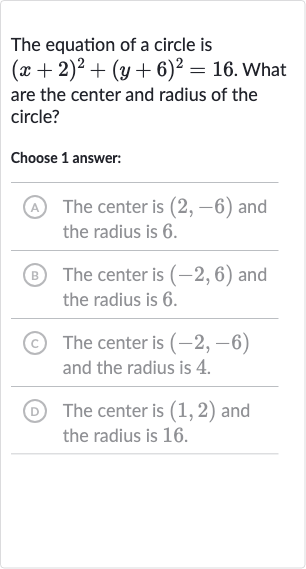
The equation of a circle is (x+2)^(2)+(y+6)^(2)=16. What are the center and radius of the circle? Choose 1 answer: (A) The center is (2,-6) and the radius is 6 . (B) The center is (-2,6) and the radius is 6 . (C) The center is (-2,-6) and the radius is 4 . (D) The center is (1,2) and the radius is 16 .

The equation of a circle is (x+2)2+(y+6)2=16 (x+2)^{2}+(y+6)^{2}=16 . What are the center and radius of the circle?\newlineChoose 11 answer:\newline(A) The center is (2,−6) (2,-6) and the radius is 66 .\newline(B) The center is (−2,6) (-2,6) and the radius is 66 .\newline(C) The center is (−2,−6) (-2,-6) and the radius is 44 .\newline(D) The center is (1,2) (1,2) and the radius is 1616 .

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Write a quadratic function from its x-intercepts and another pointright chevron icon

Full solution

Q. The equation of a circle is (x+2)2+(y+6)2=16 (x+2)^{2}+(y+6)^{2}=16 . What are the center and radius of the circle?\newlineChoose 11 answer:\newline(A) The center is (2,−6) (2,-6) and the radius is 66 .\newline(B) The center is (−2,6) (-2,6) and the radius is 66 .\newline(C) The center is (−2,−6) (-2,-6) and the radius is 44 .\newline(D) The center is (1,2) (1,2) and the radius is 1616 .
  1. Circle Equation Standard Form: The equation of a circle in standard form is (x−h)2+(y−k)2=r2(x - h)^2 + (y - k)^2 = r^2, where (h,k)(h, k) is the center of the circle and rr is the radius.
  2. Compare with Given Equation: Given the equation of the circle is (x+2)2+(y+6)2=16(x + 2)^2 + (y + 6)^2 = 16, we can compare it to the standard form to find the center and the radius.
  3. Find Center: The center of the circle is found by looking at the values that xx and yy are being added or subtracted by inside the parentheses. In the standard form, we subtract hh from xx and kk from yy. In our equation, we are adding 22 to xx and 66 to yy, which means yy00 and yy11. Therefore, the center is yy22.
  4. Find Radius: The radius of the circle is the square root of the value on the right side of the equation. Since the right side of the equation is 1616, we take the square root of 1616 to find the radius, which is 44.
  5. Match with Options: Now we can match our findings with the given options. The center is (−2,−6)(-2, -6) and the radius is 44, which corresponds to option (C)(C).

More problems from Write a quadratic function from its x-intercepts and another point

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 8 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 5 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 4 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

View all (99)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant