Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

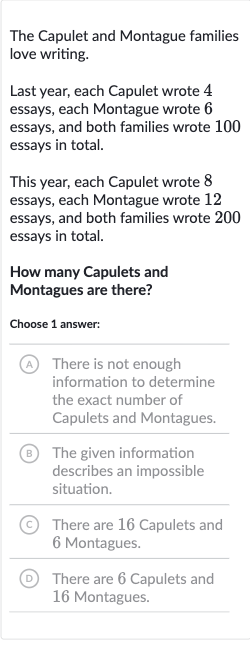
The Capulet and Montague families love writing. Last year, each Capulet wrote 4 essays, each Montague wrote 6 essays, and both families wrote 100 essays in total. This year, each Capulet wrote 8 essays, each Montague wrote 12 essays, and both families wrote 200 essays in total. How many Capulets and Montagues are there? Choose 1 answer: (A) There is not enough information to determine the exact number of Capulets and Montagues. (B) The given information describes an impossible situation. (C) There are 16 Capulets and 6 Montagues. (D) There are 6 Capulets and 16 Montagues.

The Capulet and Montague families love writing.\newlineLast year, each Capulet wrote 44 essays, each Montague wrote 66 essays, and both families wrote 100100 essays in total.\newlineThis year, each Capulet wrote 88 essays, each Montague wrote 1212 essays, and both families wrote 200200 essays in total.\newlineHow many Capulets and Montagues are there?\newlineChoose 11 answer:\newline(A) There is not enough information to determine the exact number of Capulets and Montagues.\newline(B) The given information describes an impossible situation.\newline(C) There are 1616 Capulets and 66 Montagues.\newline(D) There are 66 Capulets and 1616 Montagues.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Solve trigonometric equationsright chevron icon

Full solution

Q. The Capulet and Montague families love writing.\newlineLast year, each Capulet wrote 44 essays, each Montague wrote 66 essays, and both families wrote 100100 essays in total.\newlineThis year, each Capulet wrote 88 essays, each Montague wrote 1212 essays, and both families wrote 200200 essays in total.\newlineHow many Capulets and Montagues are there?\newlineChoose 11 answer:\newline(A) There is not enough information to determine the exact number of Capulets and Montagues.\newline(B) The given information describes an impossible situation.\newline(C) There are 1616 Capulets and 66 Montagues.\newline(D) There are 66 Capulets and 1616 Montagues.
  1. Equation 11: Let's denote the number of Capulets as CC and the number of Montagues as MM. From the first year's information, we can write the equation:\newline4C+6M=1004C + 6M = 100
  2. Equation 22: From the second year's information, we can write the equation: 8C+12M=2008C + 12M = 200
  3. Comparison: We notice that the second equation is exactly double the first equation. This means that the second equation does not provide new information; it is simply a scaled version of the first equation. Therefore, we cannot solve for CC and MM uniquely with the given information.
  4. Conclusion: Since we cannot determine the exact number of Capulets and Montagues with the given information, the correct answer is (A) There is not enough information to determine the exact number of Capulets and Montagues.

More problems from Solve trigonometric equations

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 7 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 9 months ago

View all (88)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant