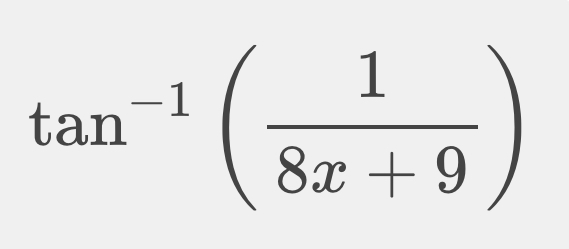AI tutor
Full solution
Q.
- Understand the problem: Understand the problem.We need to simplify the expression . This is the inverse tangent (also known as arctan) of the fraction .
- Recognize properties: Recognize the properties of the inverse tangent function.The inverse tangent function, , does not have algebraic simplifications like the ones we use for powers or roots. It is a trigonometric function that gives us an angle whose tangent is . Therefore, the expression is already in its simplest form as a function of .
- Check for simplifications: Check for any possible simplifications. Since the expression inside the inverse tangent function is a simple fraction and cannot be simplified further, and there are no trigonometric identities that apply to inverse tangent functions with a variable inside, we conclude that the expression is already in its simplest form.
More problems from Evaluate integers raised to rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help