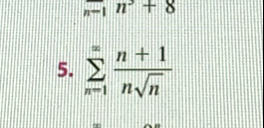AI tutor
Full solution
Q.
- Recognize Non-Standard Series: Recognize the series as a non-standard series that does not directly fit a common summation formula. We need to analyze the terms to determine if the series converges or diverges.
- Simplify Terms: Simplify the term to . This can be further simplified to .
- Split into Two Series: Split the series into two separate series: and .
- Determine Convergence: Determine the convergence or divergence of the first series . This is a p-series with , which is less than . Therefore, by the p-series test, this series diverges.
- Final Result: Since the first series diverges, there is no need to test the second series. The sum of the entire series is undefined because the series does not converge.