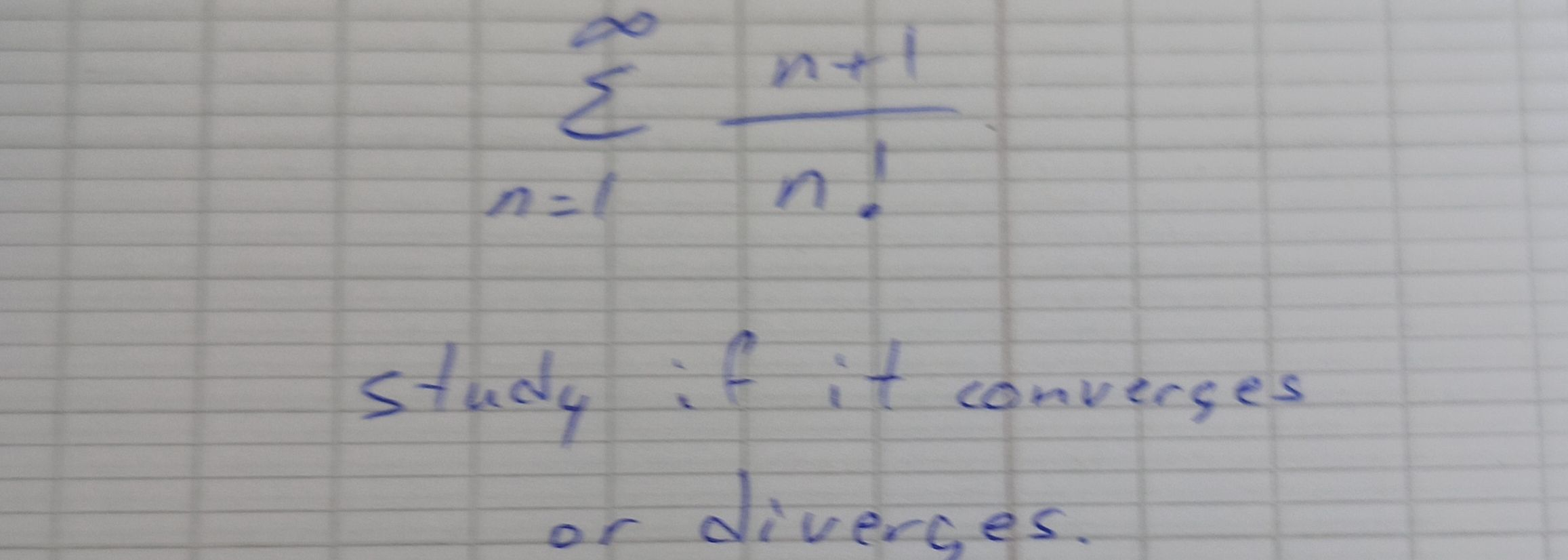AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
study if it converges or diverces.
Full solution
Q. study if it converges or diverces.
- Ratio Test Explanation: We will use the ratio test to determine if the series converges or diverges. The ratio test states that for a series , if the limit as approaches infinity of is less than , the series converges; if it is greater than , the series diverges; and if it is equal to , the test is inconclusive.
- Find General Expression: First, we need to find a general expression for , which is the th term of the series. In this case,
- Calculate : Next, we find , which is the th term of the series. This is
- Calculate : Now we calculate the ratio . This is .
- Simplify the Ratio: Simplify the ratio by multiplying the numerator and denominator by which gives us .
- Calculate Limit: Now we take the limit as approaches infinity of . As goes to infinity, the highest powers of in the numerator and denominator dominate, so the limit is , which approaches .
- Conclusion: Since the limit is , which is less than , the ratio test tells us that the series converges.
