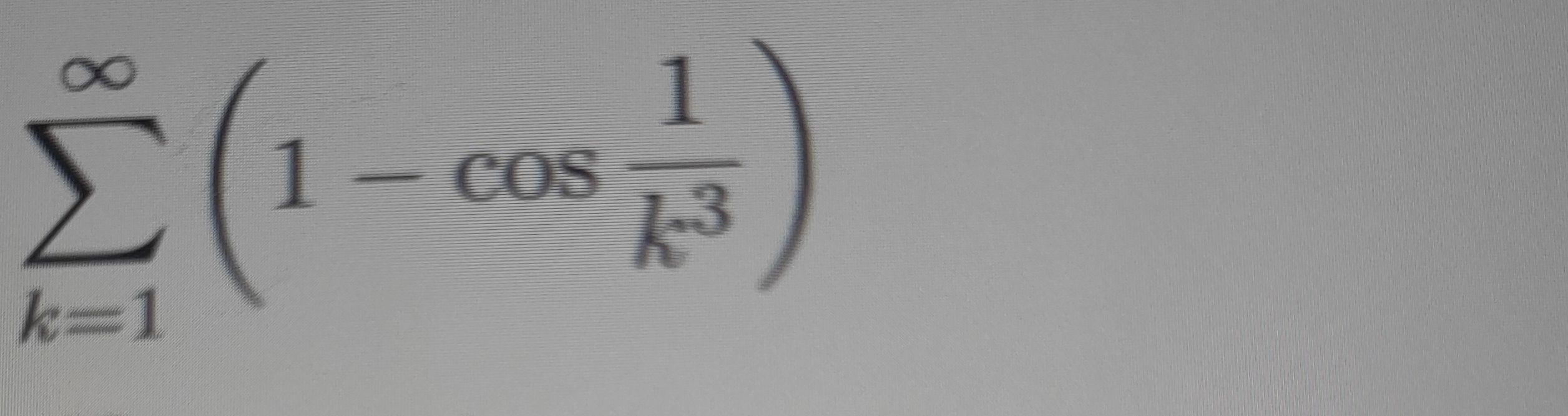sum_(k=1)^(oo)(1-cos ((1)/(k^(3))))

Question

Bytelearn · Accepted Answer

Analyze Series Behavior: We are given the infinite series sum_(k=1)^(oo)(1-cos ((1)/(k^(3)))). To find the sum of this series, we need to understand the behavior of the series as k approaches infinity. The term (1-cos ((1)/(k^(3)))) approaches 0 as k increases because the cosine of a very small number approaches 1. This suggests that the series might be convergent, but we need to analyze it further to be sure.Use Comparison Test: To analyze the convergence of the series, we can use the comparison test. We compare our series with a known convergent series. Since 1 - cos(x) is approximately x^2/2 for small x, we can compare our series to the series sum_(k=1)^(oo)(1/2k^6), which is a p-series with p = 6. A p-series is convergent if p > 1, so our comparison series is convergent.Show Inequality Holds: We need to show that for all k, (1-cos ((1)/(k^(3)))) <= (1/2k^6). This is true for large k because the second-order Taylor expansion of cos(x) around 0 is 1 - x^2/2 + O(x^4), and the term O(x^4) becomes negligible for large k. Therefore, our series is less than or equal to a convergent series term by term for large k.Conclude Convergence: Since our series is less than a convergent series, by the comparison test, our series is also convergent. However, finding the exact sum of the series is not straightforward because the cosine function does not have a simple sum when taken over an infinite series like this one. We can conclude that the series converges, but we cannot find a closed-form for the sum.

$\sum_{k=1}^{\infty}\left(1-\cos \frac{1}{k^{3}}\right)$

Full solution

More problems from Sum of finite series starts from 1

Related topics

∑k=1∞(1−cos⁡1k3) \sum_{k=1}^{\infty}\left(1-\cos \frac{1}{k^{3}}\right) ∑k=1∞​(1−cosk31​)

$\sum_{k=1}^{\infty}\left(1-\cos \frac{1}{k^{3}}\right)$