Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

State all integer values of x in the interval 0 <= x <= 7 that satisfy the following inequality: -2x+4 >= 1 Answer: x=

State all integer values of x x in the interval 0≤x≤7 0 \leq x \leq 7 that satisfy the following inequality:\newline−2x+4≥1 -2 x+4 \geq 1 \newlineAnswer: x= x=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Inverses of sin, cos, and tan: degreesright chevron icon

Full solution

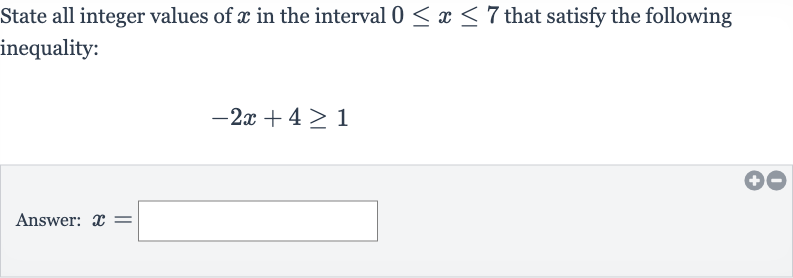
Q. State all integer values of x x in the interval 0≤x≤7 0 \leq x \leq 7 that satisfy the following inequality:\newline−2x+4≥1 -2 x+4 \geq 1 \newlineAnswer: x= x=
  1. Solve for x: First, we need to solve the inequality for xx.−2x+4≥1-2x + 4 \geq 1 Subtract 44 from both sides to isolate the term containing xx.−2x+4−4≥1−4-2x + 4 - 4 \geq 1 - 4−2x≥−3-2x \geq -3
  2. Divide by −2-2: Now, we divide both sides by −2-2 to solve for xx. Remember that dividing by a negative number reverses the inequality sign.\newline−2x/−2≤−3/−2-2x / -2 \leq -3 / -2\newlinex≤3/2x \leq 3/2
  3. Find Integer Solutions: Since we are looking for integer values of xx, we need to consider the integers that are less than or equal to 32\frac{3}{2}. The only integers that satisfy this condition in the given interval 0≤x≤70 \leq x \leq 7 are 00 and 11.

More problems from Inverses of sin, cos, and tan: degrees

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 1 month ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 2 months ago

View all (25)