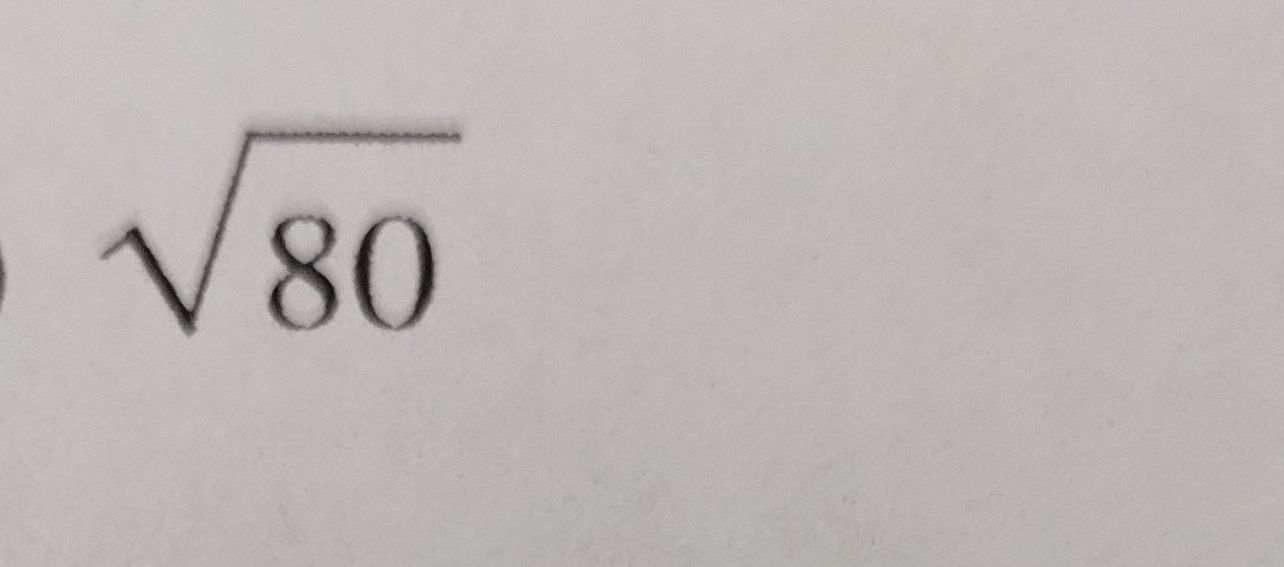Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

sqrt80

$\sqrt{80}$

View step-by-step help

View step-by-step help

Roots of integers

Full solution

Q.

\sqrt{80}

Factorize $80$ : Factor $80$ into its prime factors to simplify the square root. $\newline$ $80 = 2 \times 40$ $\newline$ $80 = 2 \times 2 \times 20$ $\newline$ $80 = 2 \times 2 \times 2 \times 10$ $\newline$ $80 = 2 \times 2 \times 2 \times 2 \times 5$ $\newline$ $80 = 2^4 \times 5$
Group Perfect Squares: Group the prime factors into pairs of equal factors to find perfect squares. $\newline$ We have four $2$ 's, which can be grouped into two pairs: $(2 \times 2)$ and $(2 \times 2)$ . $\newline$ Each pair of $2$ 's is a perfect square, so we can take the square root of each pair. $\newline$ $\sqrt{80} = \sqrt{2^4 \times 5} = \sqrt{2^2 \times 2^2 \times 5}$
Take Square Roots: Take the square root of each group of perfect squares and the remaining prime factor. $\newline$ $\sqrt{2^2 \times 2^2 \times 5} = \sqrt{2^2} \times \sqrt{2^2} \times \sqrt{5}$ $\newline$ $\sqrt{2^2} = 2$ and $\sqrt{5}$ remains as it is because $5$ is not a perfect square. $\newline$ So, $\sqrt{80} = 2 \times 2 \times \sqrt{5}$
Multiply and Simplify: Multiply the square roots of the perfect squares and write the final simplified form. $\newline$ $2 \times 2 = 4$ $\newline$ Therefore, $\sqrt{80} = 4 \times \sqrt{5}$

More problems from Roots of integers

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 2 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 2 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 2 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 month ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 2 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 2 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 2 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 2 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 4 months ago