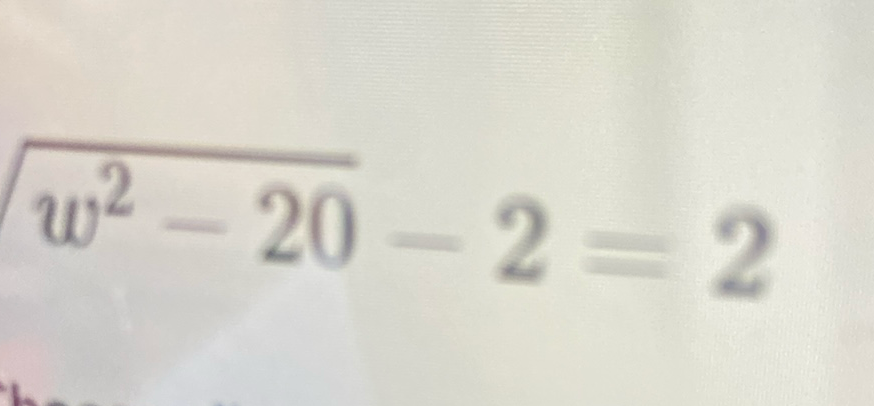AI tutor
Full solution
Q.
- Isolate square root: First, isolate the square root on one side of the equation by adding to both sides.
- Simplify equation: Simplify both sides of the equation.
- Square both sides: Now, square both sides of the equation to eliminate the square root.
- Calculate squares: Calculate the squares on both sides.
- Add : Next, add to both sides to isolate the term.
- Isolate term: Simplify both sides of the equation.
- Take square root: Take the square root of both sides to solve for . Remember that taking the square root of a number yields both a positive and negative solution. or
- Calculate solutions: Calculate the square root of . or