AI tutor
Full solution
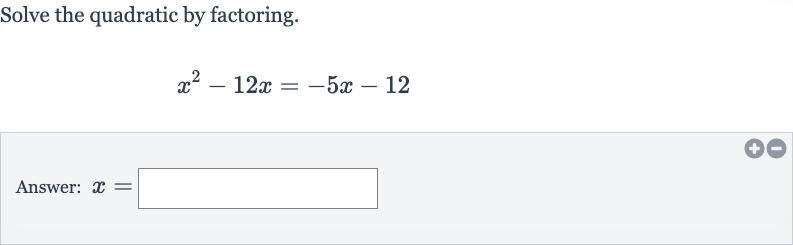
Q. Solve the quadratic by factoring.Answer:
- Move to Standard Form: Write the equation in standard form by moving all terms to one side of the equation.Add and to both sides to get:Combine like terms:
- Factor the Quadratic Equation: Factor the quadratic equation.We need to find two numbers that multiply to (the constant term) and add up to (the coefficient of the term).The numbers that satisfy these conditions are and .So we can factor the quadratic as:
- Solve for x: Solve for x by setting each factor equal to zero. or If , then .If , then .