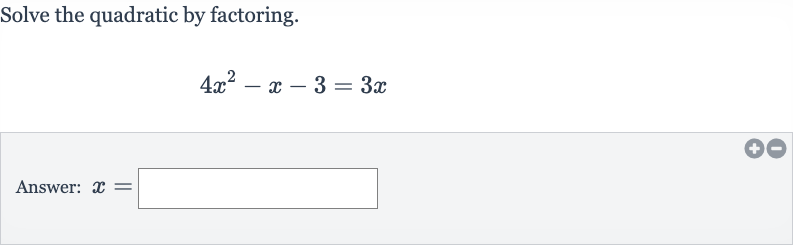
Solve the quadratic by factoring. 4x^(2)-x-3=3x Answer: x=

Question

Solve the quadratic by factoring.  4x^(2)-x-3=3x Answer:  x=

Bytelearn · Accepted Answer

Move Terms to One Side: Move all terms to one side of the equation to set the equation to zero. Subtract 3x from both sides to get 4x^2 - x - 3 - 3x = 0. Combine like terms to get 4x^2 - 4x - 3 = 0.Factor Quadratic Equation: Factor the quadratic equation 4x^2 - 4x - 3. We need to find two numbers that multiply to (4)(-3) = -12 and add up to -4. The numbers -6 and +2 satisfy these conditions because -6 * 2 = -12 and -6 + 2 = -4.Rewrite Middle Term: Rewrite the middle term using the numbers found in Step 2. 4x^2 - 4x - 3 can be written as 4x^2 - 6x + 2x - 3.Factor by Grouping: Factor by grouping. Group the first two terms and the last two terms separately. (4x^2 - 6x) + (2x - 3) Factor out the common factor of 2x from the first group and 1 from the second group. 2x(2x - 3) + 1(2x - 3)Set Factors Equal to Zero: Factor out the common binomial factor. The common binomial factor is (2x - 3). (2x - 3)(2x + 1)Set each factor equal to zero and solve for x. 2x - 3 = 0 and 2x + 1 = 0 For 2x - 3 = 0, add 3 to both sides to get 2x = 3, then divide by 2 to get x = 3/2. For 2x + 1 = 0, subtract 1 from both sides to get 2x = -1, then divide by 2 to get x = -1/2.

Solve the quadratic by factoring. $\newline$ $4 x^{2}-x-3=3 x$ $\newline$ Answer: $x=$

Full solution

More problems from Factor quadratics with other leading coefficients

Related topics

Solve the quadratic by factoring.\newline4x2−x−3=3x 4 x^{2}-x-3=3 x 4x2−x−3=3x\newlineAnswer: x= x= x=

Solve the quadratic by factoring. $\newline$ $4 x^{2}-x-3=3 x$ $\newline$ Answer: $x=$