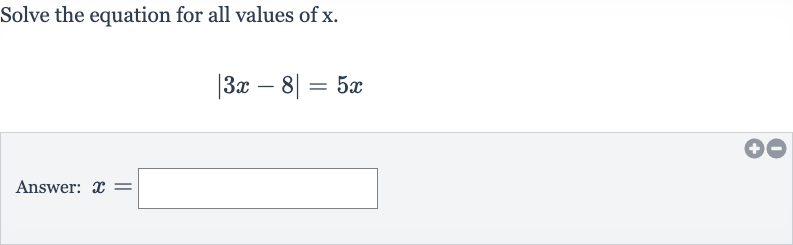
Solve the equation for all values of x. |3x-8|=5x Answer: x=

Question

Solve the equation for all values of  x.  |3x-8|=5x Answer:  x=

Bytelearn · Accepted Answer

Consider Two Cases: We have the equation |3x - 8| = 5x. To solve this, we need to consider two cases because the absolute value expression can be positive or negative.First Case: Non-Negative Expression: First case is when the expression inside the absolute value is non-negative, which means 3x - 8 >= 0. In this case, we can drop the absolute value bars and solve 3x - 8 = 5x.Solve for x: Subtract 3x from both sides of the equation 3x - 8 = 5x to get -8 = 2x.Check x = -4: Divide both sides by 2 to isolate x, which gives us x = -4.Second Case: Negative Expression: We need to check if x = -4 satisfies the original equation |3x - 8| = 5x. Substitute x = -4 into 3x - 8 to get 3(-4) - 8 = -12 - 8 = -20. The absolute value of -20 is 20, which is not equal to 5(-4) = -20. Therefore, x = -4 does not satisfy the original equation.Solve for x: The second case is when the expression inside the absolute value is negative, which means 3x - 8 < 0. In this case, we solve the equation -(3x - 8) = 5x.Check x = 1: Distribute the negative sign inside the parentheses to get -3x + 8 = 5x.Add 3x to both sides of the equation -3x + 8 = 5x to get 8 = 8x.Divide both sides by 8 to isolate x, which gives us x = 1.We need to check if x = 1 satisfies the original equation |3x - 8| = 5x. Substitute x = 1 into 3x - 8 to get 3(1) - 8 = 3 - 8 = -5. The absolute value of -5 is 5, which is equal to 5(1) = 5. Therefore, x = 1 does satisfy the original equation.

Solve the equation for all values of $x$ . $\newline$ $|3 x-8|=5 x$ $\newline$ Answer: $x=$

Full solution

More problems from Evaluate absolute value expressions

Related topics

Solve the equation for all values of x x x.\newline∣3x−8∣=5x |3 x-8|=5 x ∣3x−8∣=5x\newlineAnswer: x= x= x=

Solve the equation for all values of $x$ . $\newline$ $|3 x-8|=5 x$ $\newline$ Answer: $x=$