Full solution
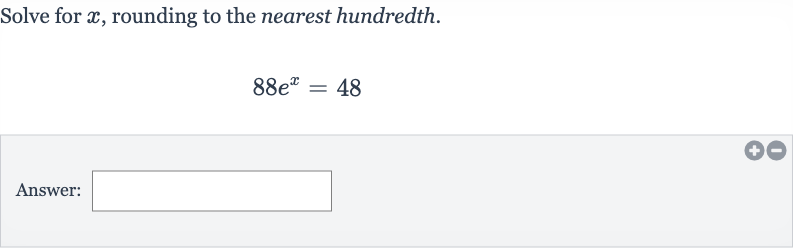
Q. Solve for , rounding to the nearest hundredth.Answer:
- Isolate exponential term: Isolate the exponential term by dividing both sides of the equation by .
- Simplify fraction: Simplify the fraction on the right-hand side of the equation.
- Take natural logarithm: Take the natural logarithm of both sides to solve for x.
- Use calculator: Use a calculator to find the value of the natural logarithm of /.
- Round result: Round the result to the nearest hundredth.
More problems from Find trigonometric functions using a calculator
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help