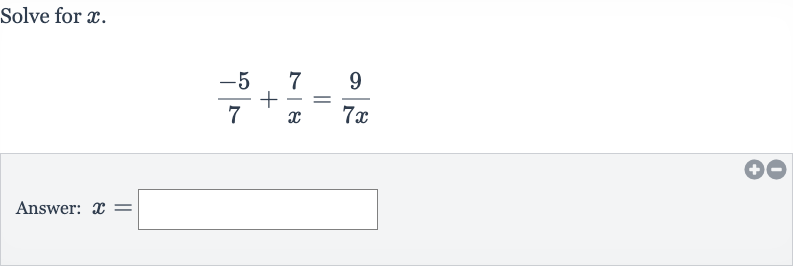Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for x. (-5)/(7)+(7)/(x)=(9)/(7x) Answer: x=

Solve for x x .\newline−57+7x=97x \frac{-5}{7}+\frac{7}{x}=\frac{9}{7 x} \newlineAnswer: x= x=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Partial sums of arithmetic seriesright chevron icon

Full solution

Q. Solve for x x .\newline−57+7x=97x \frac{-5}{7}+\frac{7}{x}=\frac{9}{7 x} \newlineAnswer: x= x=
  1. Write Equation: Write down the equation.\newline rac{-5}{7} + rac{7}{x} = rac{9}{7x}
  2. Find Common Denominator: Find a common denominator for the terms on the left side of the equation, which is 7x7x.−5x7x+497x=97x\frac{-5x}{7x} + \frac{49}{7x} = \frac{9}{7x}
  3. Combine Fractions: Combine the fractions on the left side of the equation. (−5x)+497x=97x\frac{{(-5x) + 49}}{{7x}} = \frac{9}{{7x}}
  4. Set Numerators Equal: Since the denominators are the same, we can set the numerators equal to each other.\newline−5x+49=9-5x + 49 = 9
  5. Subtract and Isolate: Subtract 4949 from both sides of the equation to isolate the term with xx.\newline−5x+49−49=9−49-5x + 49 - 49 = 9 - 49\newline−5x=−40-5x = -40
  6. Divide to Solve: Divide both sides of the equation by −5-5 to solve for xx.x=−40−5x = \frac{-40}{-5}x=8x = 8

More problems from Partial sums of arithmetic series

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 1 month ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 2 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 1 month ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 1 month ago

View all (13)