Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for
b. Express your answer in simplest radical form if necessary.

b=root(3)(-73)*root(3)(-73)*root(3)(-73)
Answer:
b=

Solve for $b$ . Express your answer in simplest radical form if necessary. $\newline$ $b=\sqrt[3]{-73} \cdot \sqrt[3]{-73} \cdot \sqrt[3]{-73}$ $\newline$ Answer: $b=$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

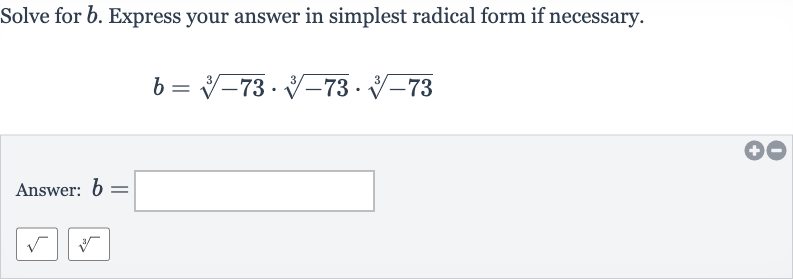
Q. Solve for

b

. Express your answer in simplest radical form if necessary.

\newline

b=\sqrt[3]{-73} \cdot \sqrt[3]{-73} \cdot \sqrt[3]{-73}

\newline

Answer:

b=

Multiply radicands under cube root: We have $b=\sqrt[3]{-73}\times\sqrt[3]{-73}\times\sqrt[3]{-73}$ . To simplify, we multiply the radicands together under a single cube root.
Calculate radicand: $b=\sqrt[3]{(-73)\cdot(-73)\cdot(-73)}$ . When we multiply $-73$ by itself three times, we get $-73\cdot-73\cdot-73$ .
Final result: Calculating $-73\times-73\times-73$ gives us $-389017$ . $\newline$ So, $b=\sqrt[3]{-389017}$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant