AI tutor
Full solution
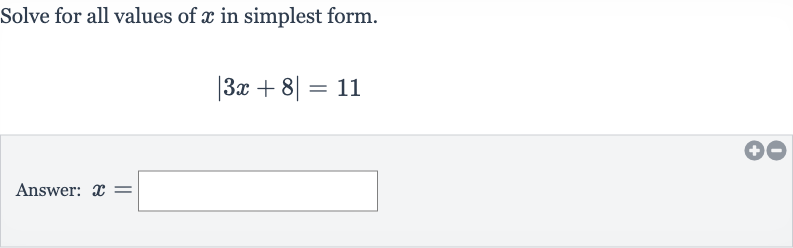
Q. Solve for all values of in simplest form.Answer:
- Absolute Value Equation: We have the absolute value equation . The absolute value of a number is the distance of that number from zero on the number line, which means it is always non-negative. Therefore, can either be or .
- Case : Positive or Zero: First, let's consider the case when is positive or zero, which gives us .Subtract from both sides to isolate the term with .
- Case : Negative: Now, divide both sides by to solve for .This is our first solution.
- First Solution: Next, let's consider the case when is negative, which gives us .Subtract from both sides to isolate the term with .
- Second Solution: Now, divide both sides by to solve for .This is our second solution.
More problems from Evaluate absolute value expressions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help