AI tutor
Full solution
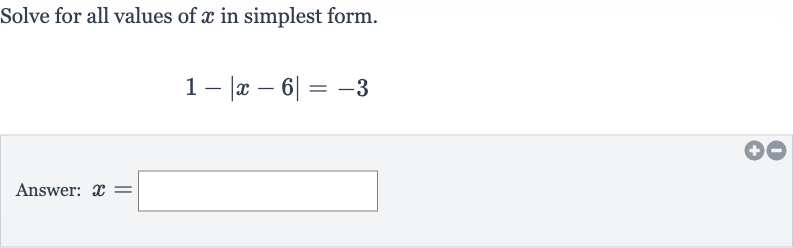
Q. Solve for all values of in simplest form.Answer:
- Write Equation: Write down the given equation.We have the equation .Let's isolate the absolute value expression on one side of the equation.
- Isolate Absolute Value: Add |x - 6| ) to both sides of the equation to isolate the absolute value expression.\(\newline\$1 - |x - 6| + |x - 6| = -3 + |x - 6|\)\(\newline\)This simplifies to:\(\newline\)\(1 = -3 + |x - 6|\)
- Subtract to Solve: Now, subtract \(-3\) from both sides to solve for \(|x - 6|\).\(\newline\)\(1 - (-3) = |x - 6|\)\(\newline\)This simplifies to:\(\newline\)\(4 = |x - 6|\)
- Absolute Value Equation: Solve the absolute value equation.\(\newline\)The equation \(|x - 6| = 4\) means that the expression inside the absolute value, \(x - 6\), can either be \(4\) or \(-4\).
- Set Up Equations: Set up two separate equations to solve for \(x\).\(x - 6 = 4\) or \(x - 6 = -4\)
- Solve First Equation: Solve the first equation \(x - 6 = 4\). Add \(6\) to both sides of the equation: \(x - 6 + 6 = 4 + 6\) This simplifies to: \(x = 10\)
- Solve Second Equation: Solve the second equation \(x - 6 = -4\). Add \(6\) to both sides of the equation: \(x - 6 + 6 = -4 + 6\) This simplifies to: \(x = 2\)
More problems from Evaluate absolute value expressions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help