AI tutor
Full solution
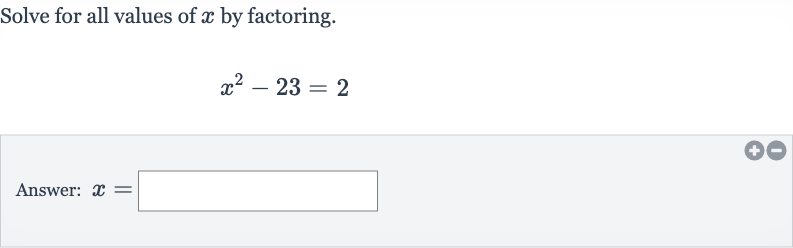
Q. Solve for all values of by factoring.Answer:
- Add : Add to both sides of the equation to isolate the term.We have the equation . To solve for , we first want to isolate the term on one side of the equation. We do this by adding to both sides of the equation.
- Take square root: Take the square root of both sides of the equation to solve for .Now that we have , we can take the square root of both sides to solve for . Remember that taking the square root of a number gives us two solutions: one positive and one negative.
- Check solutions: Check the solutions in the original equation.We have found that . We should substitute these values back into the original equation to ensure they are correct.For :, which is true.For :, which is also true.Both solutions satisfy the original equation.