AI tutor
Full solution
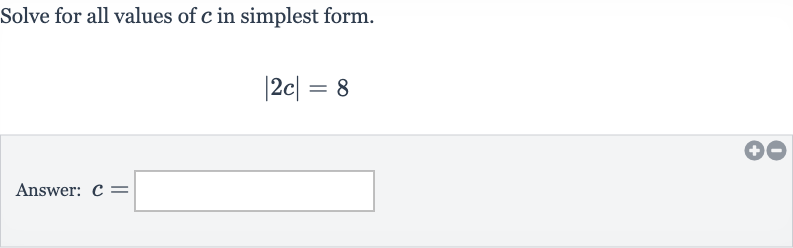
Q. Solve for all values of in simplest form.Answer:
- Given Equation: We are given the absolute value equation . The absolute value of a number is always non-negative, and it represents the distance of that number from zero on the number line. To solve for , we need to consider both the positive and negative scenarios that could result in an absolute value of .
- Positive Scenario: First, let's consider the positive scenario. If the inside of the absolute value, which is , is positive, then we can write the equation without the absolute value as:Now, we solve for by dividing both sides of the equation by .This is one possible solution for .
- Negative Scenario: Next, let's consider the negative scenario. If the inside of the absolute value, which is , is negative, then the absolute value is equal to the negative of . We can write the equation as:Now, we solve for by dividing both sides of the equation by .This is another possible solution for .
More problems from Evaluate absolute value expressions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help