AI tutor
Full solution
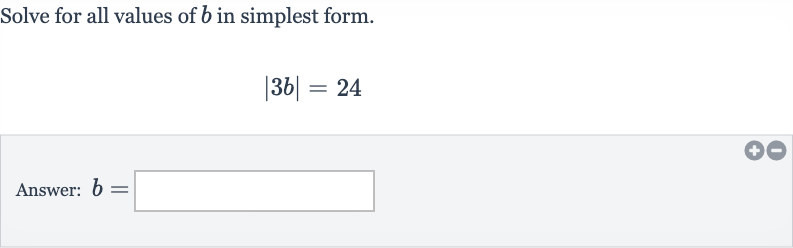
Q. Solve for all values of in simplest form.Answer:
- Understand absolute value equation: Understand the absolute value equation |3b| = 24").\(\newlineThe absolute value of a number is its distance from zero on the number line, regardless of direction. Therefore, \$3b\) can be either \(24\) or \(-24\).
- Set up separate equations: Set up two separate equations to solve for \(b\). Since \(|3b|\) can be either \(24\) or \(-24\), we have: \(3b = 24\) or \(3b = -24\)
- Solve first equation: Solve the first equation \(3b = 24\).\(\newline\)Divide both sides by \(3\) to isolate \(b\).\(\newline\)\(b = \frac{24}{3}\)\(\newline\)\(b = 8\)
- Solve second equation: Solve the second equation \(3b = -24\).\(\newline\)Divide both sides by \(3\) to isolate \(b\).\(\newline\)\(b = -24 / 3\)\(\newline\)\(b = -8\)
More problems from Evaluate absolute value expressions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help