Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for all real values of
x.

x^(2)-9=0
Answer:
x=

Solve for all real values of $x$ . $\newline$ $x^{2}-9=0$ $\newline$ Answer: $x=$ $\newline$

View step-by-step help

View step-by-step help

Solve a quadratic equation using square roots

Full solution

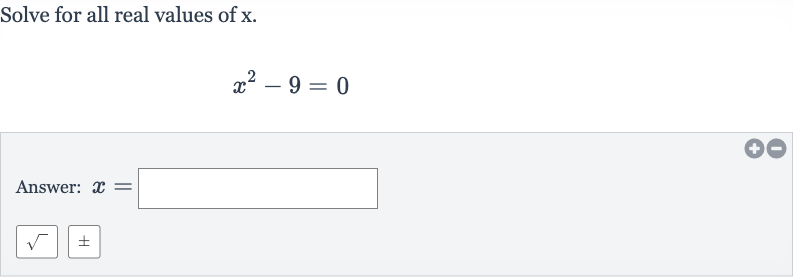
Q. Solve for all real values of

x

.

\newline

x^{2}-9=0

\newline

Answer:

x=

\newline

Set up the equation: Set up the equation. $\newline$ We have the equation $x^{2} - 9 = 0$ . $\newline$ To solve for $x$ , we need to find the values that make this equation true.
Factor the left side: Factor the left side of the equation. $\newline$ The left side of the equation is a difference of squares, which can be factored into $(x + 3)(x - 3)$ . $\newline$ So, $x^{2} - 9 = (x + 3)(x - 3)$ .
Set each factor equal: Set each factor equal to zero. $\newline$ Since the product of the factors is zero, we can set each factor equal to zero and solve for $x$ . $\newline$ $x + 3 = 0$ or $x - 3 = 0$ .
Solve each equation for $x$ : Solve each equation for $x$ . For the first equation, $x + 3 = 0$ , we subtract $3$ from both sides to get $x = -3$ . For the second equation, $x - 3 = 0$ , we add $3$ to both sides to get $x = 3$ .

More problems from Solve a quadratic equation using square roots

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 1 month ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 1 month ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 1 month ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 1 month ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 1 month ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 1 month ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 2 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 2 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 2 months ago