Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve by completing the square. 2k^(2)+12 k+2=0 Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth. k= ◻ or k= ◻

Solve by completing the square.\newline2k2+12k+2=0 2 k^{2}+12 k+2=0 \newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newlinek= k= □ \square or k= k= □ \square \newline

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Solve a quadratic equation by completing the squareright chevron icon

Full solution

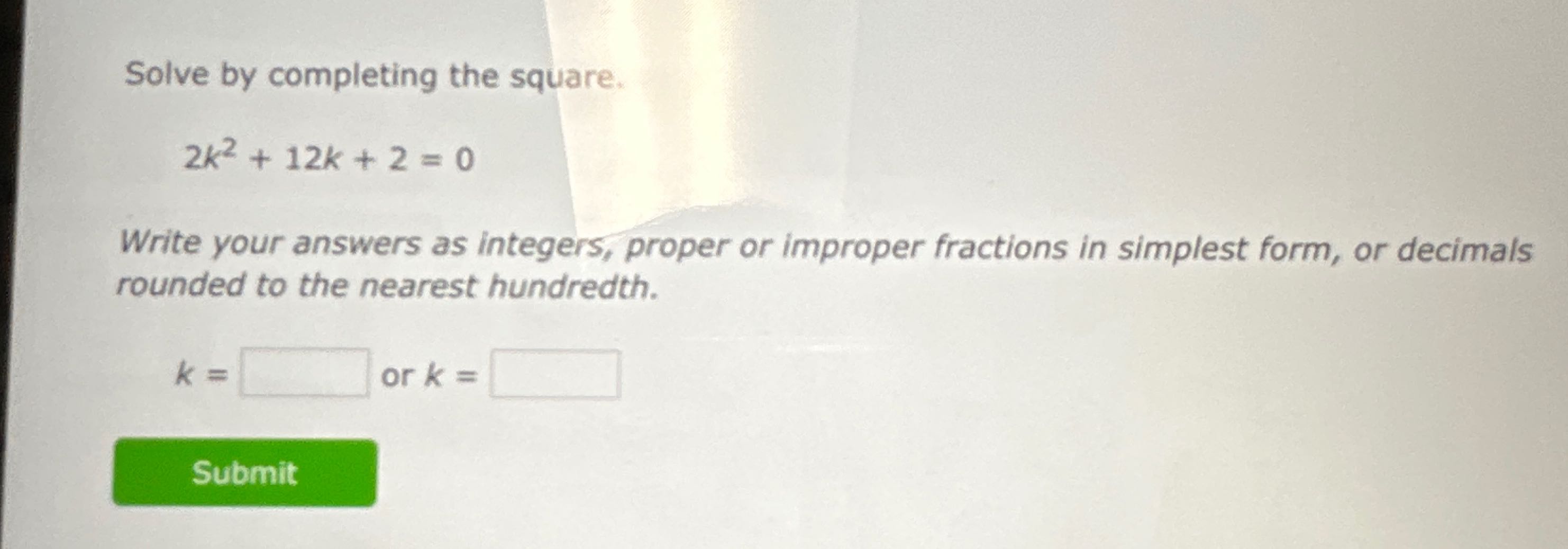
Q. Solve by completing the square.\newline2k2+12k+2=0 2 k^{2}+12 k+2=0 \newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newlinek= k= □ \square or k= k= □ \square \newline
  1. Divide and Simplify: Step 11: Start by dividing the entire equation by 22 to simplify the coefficients.\newline2k2+12k+2=02k^2 + 12k + 2 = 0 becomes k2+6k+1=0k^2 + 6k + 1 = 0.
  2. Complete the Square: Step 22: To complete the square, calculate (b2)2(\frac{b}{2})^2 where bb is the coefficient of kk. Here, b=6b = 6, so (62)2=9(\frac{6}{2})^2 = 9. Add and subtract 99 inside the equation. k2+6k+9−9+1=0k^2 + 6k + 9 - 9 + 1 = 0 simplifies to (k+3)2−8=0(k + 3)^2 - 8 = 0.
  3. Isolate Perfect Square Term: Step 33: Isolate the perfect square term by moving −8-8 to the right side of the equation.\newline(k+3)2=8(k + 3)^2 = 8.
  4. Take Square Root: Step 44: Take the square root of both sides, remembering to include both the positive and negative roots.\newlinek+3=±8k + 3 = \pm\sqrt{8}.
  5. Simplify Square Root: Step 55: Simplify 8\sqrt{8} to 222\sqrt{2} (since 8=4×2=22\sqrt{8} = \sqrt{4\times2} = 2\sqrt{2}).\newlinek+3=±22.k + 3 = \pm2\sqrt{2}.
  6. Solve for k: Step 66: Solve for k by subtracting 33 from both sides.\newlinek=−3±22.k = -3 \pm 2\sqrt{2}.

More problems from Solve a quadratic equation by completing the square

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 1 month ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 1 month ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 1 month ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

View all (180)