Full solution
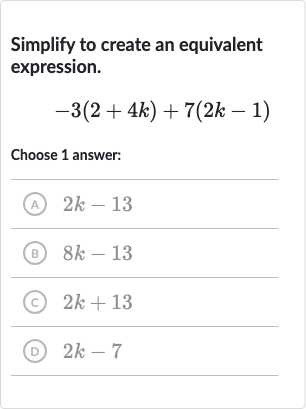
Q. Simplify to create an equivalent expression.Choose answer:(A) (B) (C) (D)
- Distribute : First, distribute the across the terms inside the first set of parentheses.So the expression becomes:
- Distribute : Next, distribute the across the terms inside the second set of parentheses.So the expression now becomes:
- Combine like terms: Combine like terms by adding/subtracting the constants and the coefficients of . (combining the constants) (combining the coefficients of )So the expression simplifies to:
- Check answer choices: Check the answer choices to see which one matches the simplified expression.The correct answer is (A) .