Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify to a single trig function with no denominator. sin^(2)theta*csc theta Answer: theta

Simplify to a single trig function with no denominator.\newlinesin⁡2θ⋅csc⁡θ \sin ^{2} \theta \cdot \csc \theta \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Simplify expressions using trigonometric identitiesright chevron icon

Full solution

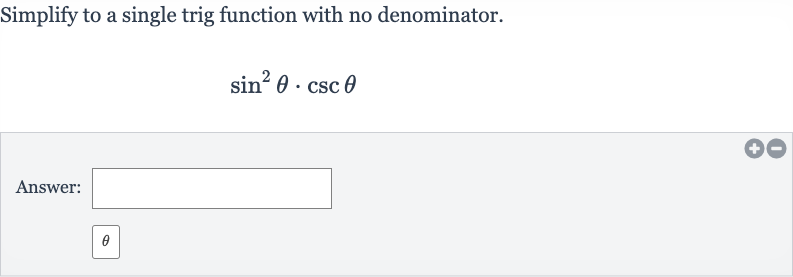
Q. Simplify to a single trig function with no denominator.\newlinesin⁡2θ⋅csc⁡θ \sin ^{2} \theta \cdot \csc \theta \newlineAnswer:
  1. Express csc⁡(θ)\csc(\theta): Express csc⁡(θ)\csc(\theta) in terms of sin⁡(θ)\sin(\theta) as csc⁡(θ)=1sin⁡(θ)\csc(\theta) = \frac{1}{\sin(\theta)}.
  2. Substitute csc⁡(θ)\csc(\theta): Substitute csc⁡(θ)\csc(\theta) with 1sin⁡(θ)\frac{1}{\sin(\theta)} in the given expression to get sin⁡2θ⋅(1sin⁡(θ))\sin^{2}\theta \cdot \left(\frac{1}{\sin(\theta)}\right).
  3. Simplify expression: Simplify sin⁡2θ×(1sin⁡(θ))\sin^{2}\theta \times \left(\frac{1}{\sin(\theta)}\right) by canceling one sin⁡(θ)\sin(\theta) in the numerator with the sin⁡(θ)\sin(\theta) in the denominator to get sin⁡(θ)\sin(\theta).

More problems from Simplify expressions using trigonometric identities

Question
If cos⁡(θ)=817 \cos(\theta)=\frac{8}{17} and 0∘<θ<90∘ 0^\circ<\theta<90^\circ , what is sec⁡(θ) \sec(\theta) ? Write your answer in simplified, rationalized form. sec⁡(θ)= \sec(\theta)= ______
Get tutor helpright-arrow

Posted 3 months ago

Question
cos⁡(x)=−0.3\cos(x) = -0.3. What is sin⁡(90∘−x)\sin(90^\circ - x)? ____
Get tutor helpright-arrow

Posted 3 months ago

Question
If csc⁡(θ)=178 \csc(\theta) = \frac{17}{8} and 0∘<θ<90∘ 0^\circ < \theta < 90^\circ , what is tan⁡(θ) \tan(\theta) ?\newlineWrite your answer in simplified, rationalized form.\newlinetan⁡(θ)= \tan(\theta) = ______\newline
Get tutor helpright-arrow

Posted 3 months ago

Question
Is the sine function even or odd?\newlineChoices:\newline[A]even\text{[A]even}\newline[B]odd\text{[B]odd}
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the sentence as an equation. \newline8989 is equal to the quotient of yy and 1717 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the sentence as an equation. \newline4545 is equal to the quotient of zz and 55 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for hh. \newline h2+24h=0h^2 + 24h = 0 \newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas. \newline h=h = _____
Get tutor helpright-arrow

Posted 4 months ago

Question
h2−4h=0h^2 - 4h = 0
Get tutor helpright-arrow

Posted 2 months ago

Question
Combine the like terms to create an equivalent expression:\newline−k−(−8k)=□-k-(-8k)=\square
Get tutor helpright-arrow

Posted 4 months ago

Question
Which of the following degree measures is equal to 5π 5 \pi radians?\newline(The number of degrees of arc in a circle is 360360 . The number of radians of arc in a circle is 2π 2 \pi .)\newlineChoose 11 answer:\newline(A) 144∘ 144^{\circ} \newline(B) 900∘ 900^{\circ} \newline(C) 1,080∘ 1,080^{\circ} \newline(D) 1,800∘ 1,800^{\circ}
Get tutor helpright-arrow

Posted 2 months ago

View all (62)