Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(16 x^{-12} y^{-8}\right)^{-\frac{5}{4}}$ $\newline$ Answer: $\newline$

View step-by-step help

Home

Math Problems

Algebra 1

Multiplication with rational exponents

Full solution

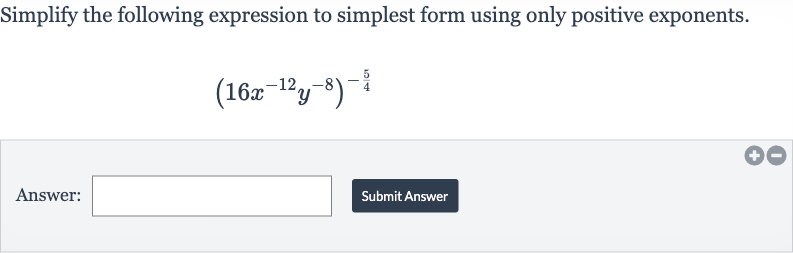
Q. Simplify the following expression to simplest form using only positive exponents.

\newline

\left(16 x^{-12} y^{-8}\right)^{-\frac{5}{4}}

\newline

Answer:

\newline

Apply negative exponent rule: Apply the negative exponent rule. $\newline$ The negative exponent rule states that $a^{-n} = \frac{1}{a^n}$ . We will apply this rule to the entire expression. $\newline$ $(16x^{-12}y^{-8})^{-\frac{5}{4}}$ $\newline$ $= \frac{1}{(16x^{-12}y^{-8})^{\frac{5}{4}}}$
Apply power of power rule: Apply the power of a power rule. $\newline$ The power of a power rule states that $(a^m)^n = a^{m*n}$ . We will apply this rule to each part of the expression inside the parentheses. $\newline$ $\frac{1}{(16^{\frac{5}{4}}) * (x^{-12 * \frac{5}{4}}) * (y^{-8 * \frac{5}{4}})}$
Calculate new exponents: Calculate the new exponents. $\newline$ Now we need to multiply the exponents by $\frac{5}{4}$ . $\newline$ $\frac{1}{(16^{\frac{5}{4}}) \cdot (x^{-15}) \cdot (y^{-10})}$
Simplify base $16$ : Simplify the base $16$ with the exponent $\frac{5}{4}$ . $16$ is $2$ to the power of $4$ , so we can rewrite $16^{\frac{5}{4}}$ as $(2^4)^{\frac{5}{4}}$ . $\frac{1}{((2^4)^{\frac{5}{4}} * x^{-15} * y^{-10})} = \frac{1}{(2^{4*\frac{5}{4}} * x^{-15} * y^{-10})} = \frac{1}{(2^5 * x^{-15} * y^{-10})} = \frac{1}{(32 * x^{-15} * y^{-10})}$
Apply negative exponent rule to $x$ and $y$ : Apply the negative exponent rule to $x$ and $y$ . We will apply the negative exponent rule to $x^{-15}$ and $y^{-10}$ to make the exponents positive. $\frac{1}{32 \times \left(\frac{1}{x^{15}}\right) \times \left(\frac{1}{y^{10}}\right)}$
Simplify the expression: Simplify the expression. $\newline$ Now we can simplify the expression by multiplying the denominators. $\newline$ $\frac{1}{32} \times \frac{1}{x^{15}} \times \frac{1}{y^{10}}$ $\newline$ = $\frac{1}{\frac{32}{x^{15} \times y^{10}}}$ $\newline$ = $\frac{x^{15} \times y^{10}}{32}$