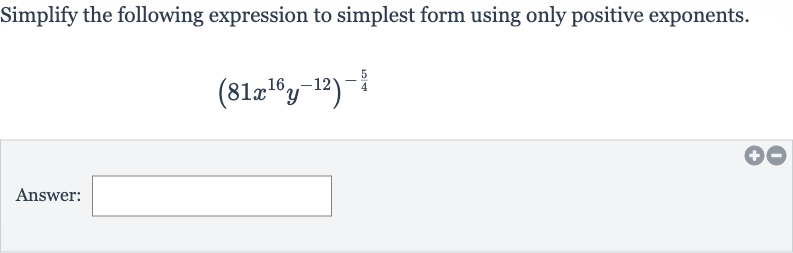
Simplify the following expression to simplest form using only positive exponents. (81x^(16)y^(-12))^(-(5)/(4)) Answer:

Question

Simplify the following expression to simplest form using only positive exponents.  (81x^(16)y^(-12))^(-(5)/(4)) Answer:

Bytelearn · Accepted Answer

Apply Negative Exponent Rule: Apply the negative exponent rule to the entire expression. The negative exponent rule states that a^(-n) = 1/(a^n). We will apply this rule to the entire expression (81x^(16)y^(-12))^(-(5)/(4)).Distribute Exponents: Distribute the exponent to each factor inside the parentheses. When raising a power to a power, you multiply the exponents. In this case, we have a product of three terms inside the parentheses, each of which will be raised to the power of -(5/4). (81x^(16)y^(-12))^(-(5)/(4)) = 81^(-(5)/(4)) * x^(16*(-(5)/(4))) * y^(-12*(-(5)/(4)))Simplify Each Term: Simplify each term separately. Now we simplify each term by multiplying the exponents. 81^(-(5)/(4)) = 1/(81^(5/4)) x^(16*(-(5)/(4))) = x^(-20) y^(-12*(-(5)/(4))) = y^(15)Convert Negative Exponents: Convert negative exponents to positive exponents. We already have y^(15) with a positive exponent. For x^(-20), we use the rule that a^(-n) = 1/(a^n) to convert the negative exponent to a positive one. x^(-20) = 1/(x^(20))Calculate 81^(5/4): Calculate 81^(5/4). To calculate 81^(5/4), we first find the fourth root of 81, which is 3, because 3^4 = 81. Then we raise 3 to the power of 5. 81^(5/4) = (3^4)^(5/4) = 3^5 = 243Write Final Expression: Write the final expression using only positive exponents. We combine the results from the previous steps to write the final expression. 1/(81^(5/4)) * 1/(x^(20)) * y^(15) = 1/(243) * 1/(x^(20)) * y^(15)

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(81 x^{16} y^{-12}\right)^{-\frac{5}{4}}$ $\newline$ Answer:

Full solution

More problems from Multiplication with rational exponents

Related topics

Simplify the following expression to simplest form using only positive exponents.\newline(81x16y−12)−54 \left(81 x^{16} y^{-12}\right)^{-\frac{5}{4}} (81x16y−12)−45​\newlineAnswer:

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(81 x^{16} y^{-12}\right)^{-\frac{5}{4}}$ $\newline$ Answer: