Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the following expression to simplest form using only positive exponents.

(81x^(-6)y^(2))^((1)/(2))
Answer:

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(81 x^{-6} y^{2}\right)^{\frac{1}{2}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

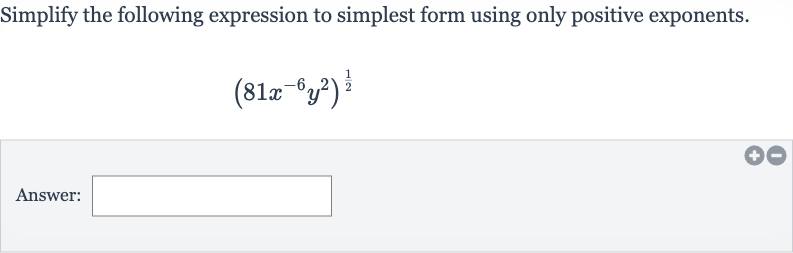
Q. Simplify the following expression to simplest form using only positive exponents.

\newline

\left(81 x^{-6} y^{2}\right)^{\frac{1}{2}}

\newline

Answer:

Apply Exponent Rule: Apply the exponent rule $(a^m)^n = a^{m*n}$ to the given expression. $\newline$ $(81x^{-6}y^{2})^{\frac{1}{2}} = 81^{\frac{1}{2}} * x^{-6*\frac{1}{2}} * y^{2*\frac{1}{2}}$
Simplify Parts: Simplify each part of the expression separately. $\newline$ $81^{\frac{1}{2}} = 9$ because $9^2 = 81$ $\newline$ $x^{-6\left(\frac{1}{2}\right)} = x^{-3}$ because $-6\left(\frac{1}{2}\right) = -3$ $\newline$ $y^{2\left(\frac{1}{2}\right)} = y^1 = y$ because $2\left(\frac{1}{2}\right) = 1$
Rewrite with Positive Exponents: Rewrite the expression with positive exponents by moving the term with a negative exponent to the denominator. $\newline$ $9 \times x^{-3} \times y = \frac{9y}{x^3}$ because $x^{-3} = \frac{1}{x^3}$
Combine Simplified Parts: Combine the simplified parts to write the final answer. $\newline$ The expression $(81x^{-6}y^{2})^{\frac{1}{2}}$ simplifies to $\frac{9y}{x^3}$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant