Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the following expression to simplest form using only positive exponents.

(125x^(3)y^(-6))^((1)/(3))
Answer:

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(125 x^{3} y^{-6}\right)^{\frac{1}{3}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

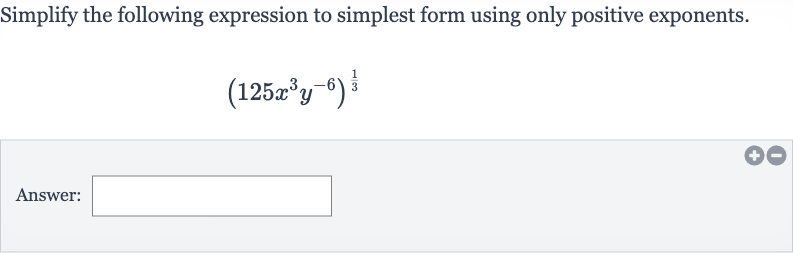
Q. Simplify the following expression to simplest form using only positive exponents.

\newline

\left(125 x^{3} y^{-6}\right)^{\frac{1}{3}}

\newline

Answer:

Understand and Apply Cube Root: Understand the expression and apply the cube root. $\newline$ We have the expression $(125x^{3}y^{-6})^{\frac{1}{3}}$ . The cube root of a number or variable is the same as raising that number or variable to the power of $\frac{1}{3}$ . We will apply this to each part of the expression inside the parentheses.
Apply Cube Root to Components: Apply the cube root to each part of the expression. $\newline$ $(125x^{3}y^{-6})^{(1)/(3)}$ can be broken down into the cube root of each component: the cube root of $125$ , the cube root of $x^3$ , and the cube root of $y^{-6}$ . $\newline$ The cube root of $125$ is $5$ , because $5^3 = 125$ . $\newline$ The cube root of $x^3$ is $x$ , because $(x^3)^{(1/3)} = x^{(3*(1/3))} = x^{(1)} = x$ . $\newline$ The cube root of $y^{-6}$ is $125$ $1$ , because $125$ $2$ .
Combine Results: Combine the results. $\newline$ Combining the results from Step $2$ , we get: $\newline$ $5 \times x \times y^{-2}$ .
Rewrite with Positive Exponents: Rewrite the expression with only positive exponents. $\newline$ Since we want the expression in simplest form with only positive exponents, we need to address the negative exponent on $y$ . To make the exponent positive, we can rewrite $y^{-2}$ as $1/(y^2)$ . $\newline$ So, the expression becomes: $\newline$ $5 \times x \times (1/(y^2))$ .
Simplify Expression: Simplify the expression. $\newline$ The expression $5 \times x \times \left(\frac{1}{y^2}\right)$ is already simplified, but we can write it more conventionally as: $\newline$ $\frac{5x}{y^2}$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant