Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the following expression to simplest form using only positive exponents.

(32x^(20)y^(-25))^(-(2)/(5))
Answer:

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(32 x^{20} y^{-25}\right)^{-\frac{2}{5}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

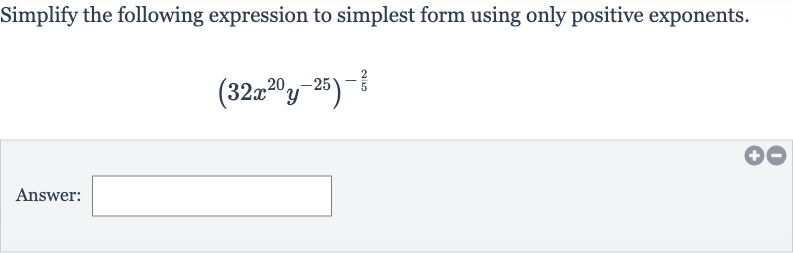
Q. Simplify the following expression to simplest form using only positive exponents.

\newline

\left(32 x^{20} y^{-25}\right)^{-\frac{2}{5}}

\newline

Answer:

Apply Negative Exponent Rule: Apply the negative exponent rule to the entire expression. $\newline$ The negative exponent rule states that $a^{-n} = \frac{1}{a^n}$ . We will apply this rule to the entire expression $(32x^{20}y^{-25})^{-\frac{2}{5}}$ .
Distribute Exponent to Factors: Distribute the exponent to each factor inside the parentheses. $\newline$ When raising a power to a power, you multiply the exponents. In this case, we have a product inside the parentheses, so we will distribute the exponent to each factor. $\newline$ $(32x^{20}y^{-25})^{-(2)/(5)} = 32^{-(2)/(5)} \times x^{20\cdot(-(2)/(5))} \times y^{-25\cdot(-(2)/(5))}$
Simplify Each Factor: Simplify each factor separately. $\newline$ Now we simplify each factor by multiplying the exponents. $\newline$ $32^{-(2)/(5)} = 1/(32^{2/5})$ $\newline$ $x^{20*(-(2)/(5))} = x^{-8} = 1/(x^8)$ $\newline$ $y^{-25*(-(2)/(5))} = y^{10}$
Calculate Fifth Root of $32$ : Calculate the fifth root of $32$ and raise it to the power of $2$ . $32^{1/5}$ is the fifth root of $32$ , which is $2$ because $2^5 = 32$ . Then we raise $2$ to the power of $2$ to get $4$ . $32^{2/5} = (32^{1/5})^2 = 2^2 = 4$
Combine Simplified Factors: Combine all the simplified factors. $\newline$ Now we combine all the factors to get the final expression with positive exponents. $\newline$ $\frac{1}{32^{\frac{2}{5}}} \times \frac{1}{x^8} \times y^{10} = \frac{1}{4 \times x^8} \times y^{10}$
Write Final Expression: Write the final simplified expression. $\newline$ The final expression is: $\newline$ $\frac{1}{4x^8} \cdot y^{10}$

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant