Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the following expression to simplest form using only positive exponents.

(32x^(25)y^(-40))^((4)/(5))
Answer:

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(32 x^{25} y^{-40}\right)^{\frac{4}{5}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

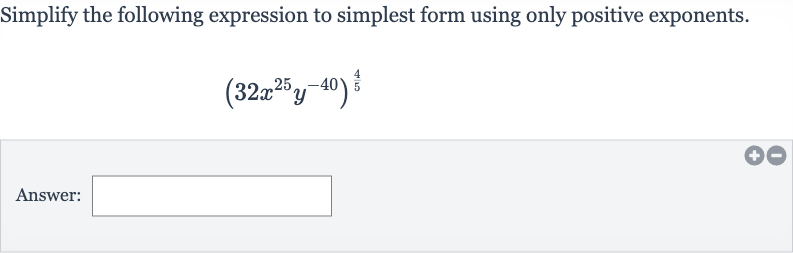
Q. Simplify the following expression to simplest form using only positive exponents.

\newline

\left(32 x^{25} y^{-40}\right)^{\frac{4}{5}}

\newline

Answer:

Apply Power to Factors: Apply the power to each factor inside the parentheses. $\newline$ When raising a power to a power, you multiply the exponents. For the numerical base $32$ , which is $2^5$ , we will apply the exponent $(4/5)$ to both the base and the exponents of $x$ and $y$ . $\newline$ $(32x^{25}y^{-40})^{(4)/(5)} = (2^5)^{4/5} * x^{25*(4/5)} * y^{-40*(4/5)}$
Simplify Exponents: Simplify the exponents. $\newline$ Now we simplify the exponents by multiplying them. $\newline$ $(2^5)^{\frac{4}{5}} = 2^{5*\left(\frac{4}{5}\right)} = 2^4$ $\newline$ $x^{25*\left(\frac{4}{5}\right)} = x^{\frac{100}{5}} = x^{20}$ $\newline$ $y^{-40*\left(\frac{4}{5}\right)} = y^{-32}$
Rewrite with Positive Exponents: Rewrite the expression with positive exponents only. $\newline$ Since we want only positive exponents, we need to take the reciprocal of $y$ to change the negative exponent to a positive one. $\newline$ $2^4 \times x^{20} \times y^{-32} = 2^4 \times x^{20} \times (1/y^{32})$
Calculate $2^4$ : Calculate the value of $2^4$ . $\newline$ $2^4 = 2 \times 2 \times 2 \times 2 = 16$
Combine for Final Answer: Combine all the parts to write the final answer. $\newline$ The final simplified expression is: $\newline$ $16 \times x^{20} \times \left(\frac{1}{y^{32}}\right)$

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant