Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the following expression to simplest form using only positive exponents.

(49x^(2)y^(8))^(-(1)/(2))
Answer:

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(49 x^{2} y^{8}\right)^{-\frac{1}{2}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Evaluate integers raised to rational exponents

Full solution

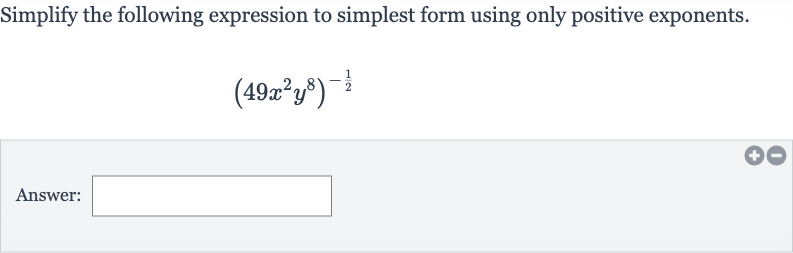
Q. Simplify the following expression to simplest form using only positive exponents.

\newline

\left(49 x^{2} y^{8}\right)^{-\frac{1}{2}}

\newline

Answer:

Apply negative exponent rule: Apply the negative exponent rule. $\newline$ The negative exponent rule states that $a^{-n} = \frac{1}{a^n}$ . We will apply this rule to the entire expression. $\newline$ $(49x^{2}y^{8})^{-\frac{1}{2}} = \frac{1}{(49x^{2}y^{8})^{\frac{1}{2}}}$
Simplify inside parentheses: Simplify the expression inside the parentheses. $\newline$ We need to find the square root of each term inside the parentheses since the exponent is $\frac{1}{2}$ . $\newline$ The square root of $49$ is $7$ , the square root of $x^2$ is $x$ , and the square root of $y^8$ is $y^4$ . $\newline$ $\frac{1}{((49x^{2}y^{8})^{\frac{1}{2}})} = \frac{1}{(7x^{1}y^{4})}$
Write final expression: Write the final expression using only positive exponents. $\newline$ Since we have already applied the negative exponent as a reciprocal in step $1$ , the final expression is already with positive exponents. $\newline$ The final simplified expression is $\frac{1}{7x y^{4}}$ .

More problems from Evaluate integers raised to rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant