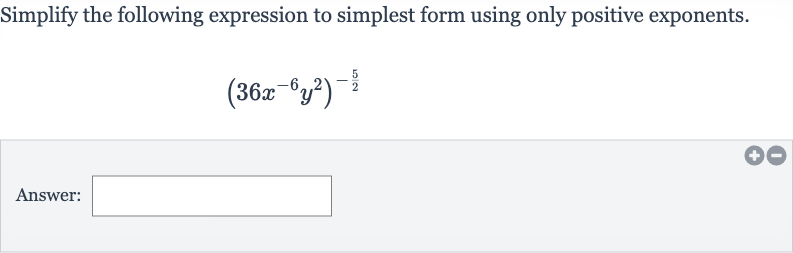
Simplify the following expression to simplest form using only positive exponents. (36x^(-6)y^(2))^(-(5)/(2)) Answer:

Question

Simplify the following expression to simplest form using only positive exponents.  (36x^(-6)y^(2))^(-(5)/(2)) Answer:

Bytelearn · Accepted Answer

Apply Negative Exponent Rule: Apply the negative exponent rule to the entire expression. The negative exponent rule states that a^(-n) = 1/(a^n). We will apply this rule to the entire expression (36x^(-6)y^(2))^(-(5)/(2)). (36x^(-6)y^(2))^(-(5)/(2)) = 1/((36x^(-6)y^(2))^(5/2))Apply Power of Power Rule: Apply the power of a power rule. The power of a power rule states that (a^m)^n = a^(m*n). We will apply this rule to each part of the expression inside the parentheses. 1/((36^(5/2))(x^(-6*5/2))(y^(2*5/2)))Simplify Exponents: Simplify the exponents. Now we will simplify the exponents by multiplying them. 1/((36^(5/2))(x^(-15))(y^(5)))Simplify Numerical Part: Simplify the numerical part of the expression. 36 is a perfect square, so we can simplify 36^(5/2) by taking the square root of 36, which is 6, and then raising it to the power of 5. 1/((6^5)(x^(-15))(y^(5)))Calculate 6^5: Calculate 6^5. 6^5 = 6*6*6*6*6 = 7776 1/((7776)(x^(-15))(y^(5)))Apply Negative Exponent Rule to x^(-15): Apply the negative exponent rule to x^(-15). The negative exponent rule states that a^(-n) = 1/(a^n). We will apply this rule to x^(-15). 1/((7776)(1/(x^(15)))(y^(5)))Combine Terms: Simplify the expression by combining the terms. Now we combine the terms under the single denominator. 1/((7776)/(x^(15))(y^(5)))Rewrite with Positive Exponents: Rewrite the expression with positive exponents only. Since we want only positive exponents, we will move x^(15) to the denominator. 1/((7776)(y^(5))(x^(15)))Check for Further Simplifications: Check for any further simplifications. There are no further simplifications possible, as 7776 is already in its simplest form, and there are no like terms to combine with x^(15) and y^(5).

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(36 x^{-6} y^{2}\right)^{-\frac{5}{2}}$ $\newline$ Answer:

Full solution

More problems from Multiplication with rational exponents

Related topics

Simplify the following expression to simplest form using only positive exponents.\newline(36x−6y2)−52 \left(36 x^{-6} y^{2}\right)^{-\frac{5}{2}} (36x−6y2)−25​\newlineAnswer:

Simplify the following expression to simplest form using only positive exponents. $\newline$ $\left(36 x^{-6} y^{2}\right)^{-\frac{5}{2}}$ $\newline$ Answer: