Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

$Simplify the expression. Write your answers using integers or improper fractions. -3k+(1)/(2)((3)/(2)k-3) Answer:$

Simplify the expression. Write your answers using integers or improper fractions. $\newline$ $-3 k+\frac{1}{2}\left(\frac{3}{2} k-3\right)$ $\newline$ Answer:

View step-by-step help

Full solution

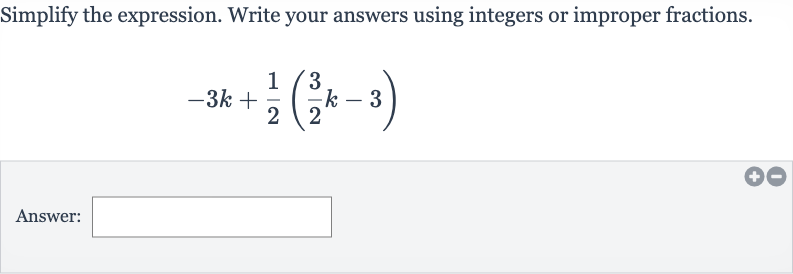
Q. Simplify the expression. Write your answers using integers or improper fractions.

\newline

-3 k+\frac{1}{2}\left(\frac{3}{2} k-3\right)

\newline

Answer:

Distribute fractions in parentheses: Distribute the $(1/2)$ across the terms inside the parentheses. $\newline$ We have the expression $-3k + (1/2)((3/2)k - 3)$ . To simplify, we first need to distribute the $(1/2)$ to both $(3/2)k$ and $-3$ . $\newline$ $-3k + (1/2)(3/2)k - (1/2)(3)$
Multiply fractions: Multiply the fractions. $\newline$ Now we multiply the fractions $(\frac{1}{2})$ and $(\frac{3}{2})k$ , and $(\frac{1}{2})$ and $3$ . $\newline$ $-3k + (\frac{1}{2} \times \frac{3}{2})k - (\frac{1}{2} \times 3)$
Simplify multiplication: Simplify the multiplication of the fractions. $\newline$ $(\frac{1}{2} \times \frac{3}{2}) = \frac{3}{4}$ and $(\frac{1}{2} \times 3) = \frac{3}{2}$ , so we substitute these back into the expression. $\newline$ $-3k + (\frac{3}{4})k - \frac{3}{2}$
Combine like terms: Combine like terms. $\newline$ We combine the terms with $k$ in them, which are $-3k$ and $(3/4)k$ . $\newline$ To combine them, we need a common denominator, which is $4$ . So we convert $-3k$ to $(-12/4)k$ . $\newline$ $(-12/4)k + (3/4)k - 3/2$
Add coefficients of $k$ : Add the coefficients of $k$ . $\newline$ Now we add $(-\frac{12}{4})$ and $(\frac{3}{4})$ together. $\newline$ $(-\frac{12}{4} + \frac{3}{4})k - \frac{3}{2}$
Simplify addition: Simplify the addition. $\newline$ $-\frac{12}{4} + \frac{3}{4} = -\frac{9}{4}$ , so we substitute this back into the expression. $\newline$ $(-\frac{9}{4})k - \frac{3}{2}$
Final simplified expression: The expression is now simplified. The simplified expression is $(-\frac{9}{4})k - \frac{3}{2}$ .