Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

$Simplify the expression. Write your answers using integers or improper fractions. -(1)/(2)((1)/(2)h+(1)/(2))+4h Answer:$

Simplify the expression. Write your answers using integers or improper fractions. $\newline$ $-\frac{1}{2}\left(\frac{1}{2} h+\frac{1}{2}\right)+4 h$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Roots of rational numbers

Full solution

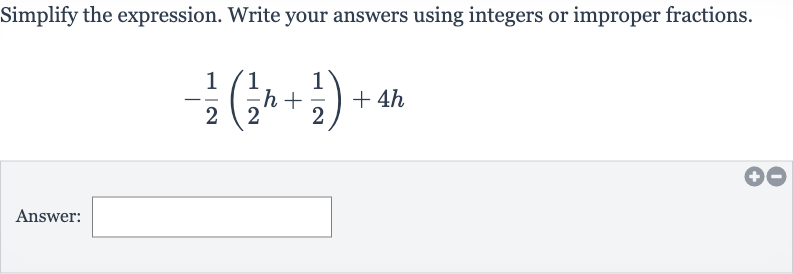
Q. Simplify the expression. Write your answers using integers or improper fractions.

\newline

-\frac{1}{2}\left(\frac{1}{2} h+\frac{1}{2}\right)+4 h

\newline

Answer:

Distribute and Simplify: First, distribute the negative one-half across the terms inside the parentheses. $\newline$ $-\frac{1}{2}(\frac{1}{2}h+\frac{1}{2}) = -\frac{1}{2}\cdot\frac{1}{2}h - \frac{1}{2}\cdot\frac{1}{2}$
Simplify Fractions: Now, simplify the multiplication of the fractions. $\newline$ $-\frac{1}{2}\times\frac{1}{2}h = -\frac{1\times1}{2\times2}h = -\frac{1}{4}h$ $\newline$ $-\frac{1}{2}\times\frac{1}{2} = -\frac{1\times1}{2\times2} = -\frac{1}{4}$
Combine Terms: Combine the simplified terms with the $4h$ term that is outside the parentheses. $\newline$ $-(\frac{1}{4})h - (\frac{1}{4}) + 4h$
Add Like Terms: Combine like terms by adding $-\frac{1}{4}h$ and $4h$ . $\newline$ $4h - \frac{1}{4}h = \frac{16}{4}h - \frac{1}{4}h = \frac{15}{4}h$
Final Simplified Expression: Now, bring down the constant term $-(1)/(4)$ . The final simplified expression is $(15/4)h - (1)/(4)$ .

More problems from Roots of rational numbers

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 1 year ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 1 year ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 1 year ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 year ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 1 year ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 1 year ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 1 year ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 1 year ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 1 year ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 1 year ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant