Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the expression to a + bi form: (-12+2i)(-3+i) Answer:

Simplify the expression to a + bi form:\newline(−12+2i)(−3+i) (-12+2 i)(-3+i) \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Write a quadratic function from its zerosright chevron icon

Full solution

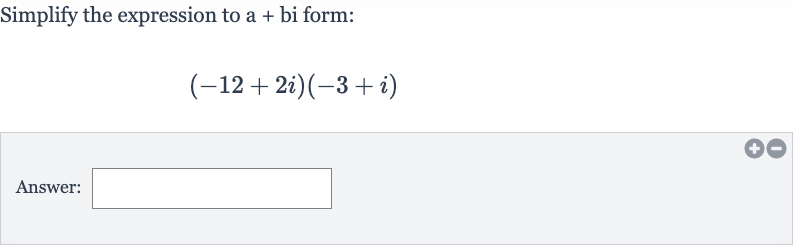
Q. Simplify the expression to a + bi form:\newline(−12+2i)(−3+i) (-12+2 i)(-3+i) \newlineAnswer:
  1. Distribute Terms: Distribute each term in the first complex number by each term in the second complex number.\newline(−12+2i)(−3+i)=(−12×−3)+(−12×i)+(2i×−3)+(2i×i)(-12+2i)(-3+i) = (-12 \times -3) + (-12 \times i) + (2i \times -3) + (2i \times i)
  2. Perform Multiplication: Perform the multiplication for each term.\newline(−12×−3)=36(-12 \times -3) = 36\newline(−12×i)=−12i(-12 \times i) = -12i\newline(2i×−3)=−6i(2i \times -3) = -6i\newline(2i×i)=2i2(2i \times i) = 2i^2
  3. Apply i2i^2 Rule: Remember that i2=−1i^2 = -1, and apply this to simplify the term with i2i^2.\newline2i2=2(−1)=−22i^2 = 2(-1) = -2
  4. Combine Like Terms: Combine like terms. \newline36+(−12i)+(−6i)+(−2)=36−2−12i−6i=34−18i36 + (-12i) + (-6i) + (-2) = 36 - 2 - 12i - 6i = 34 - 18i
  5. Final Answer: Write the final answer in a+bia + bi form.\newlineThe simplified expression is 34−18i34 - 18i.

More problems from Write a quadratic function from its zeros

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 3 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 3 months ago

View all (28)