AI tutor
Full solution
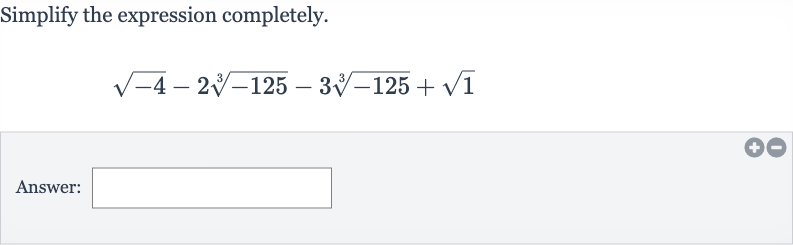
Q. Simplify the expression completely.Answer:
- Square Root of : We need to simplify each term in the expression separately. Let's start with the first term, .The square root of a negative number involves an imaginary number. The square root of is defined as the imaginary unit .So, .
- Simplify : Now let's simplify the second term, . The cube root of is because . So, .
- Simplify : Next, we simplify the third term, . Using the same logic as the previous step, .
- Square Root of : Finally, let's simplify the fourth term, .The square root of is because .So, .
- Combine Simplified Terms: Now we combine all the simplified terms to get the final simplified expression. .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help