AI tutor
Full solution
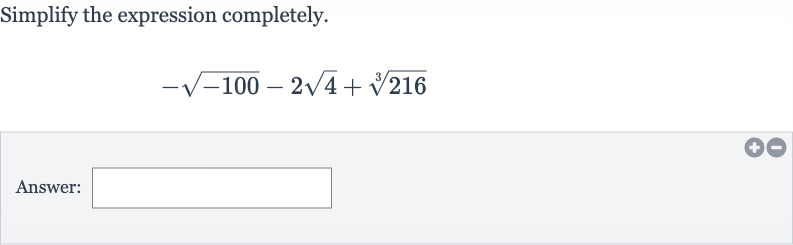
Q. Simplify the expression completely.Answer:
- Simplify : Simplify the square root of . The square root of a negative number involves an imaginary number. The square root of is the square root of times the square root of , which is , where is the imaginary unit. Calculation:
- Simplify : Simplify the square root of . The square root of is because squared is . Calculation:
- Cube root of : Simplify the cube root of .The cube root of is because cubed is .Calculation:
- Combine simplified parts: Combine all the simplified parts together.We have the expression , which simplifies to .Calculation:
- Perform arithmetic operations: Perform the arithmetic operations.Subtract from to get , and keep the separate as it involves an imaginary number.Calculation:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help