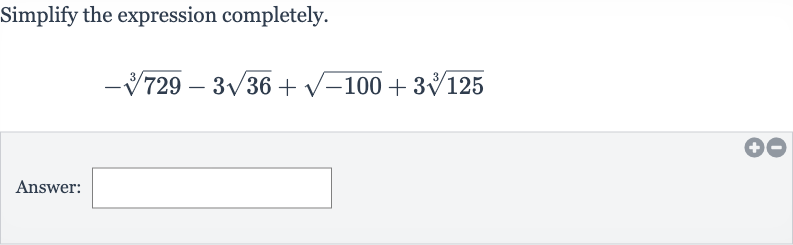AI tutor
Full solution
Q. Simplify the expression completely.Answer:
- Cube Root of : First, we will simplify each term in the expression separately, starting with the cube root of .-\sqrt[\(3]{} = -\sqrt[]{\times\times} = -\sqrt[]{^} =
- Square Root of : Next, we simplify the square root of .
- Square Root of : Now, we simplify the square root of . Since the square root of a negative number is not a real number, we will express it in terms of , where is the imaginary unit.
- Cube Root of : Finally, we simplify the cube root of .
- Combine Simplified Terms: Now we combine all the simplified terms to get the final answer.Answer =