AI tutor
Full solution
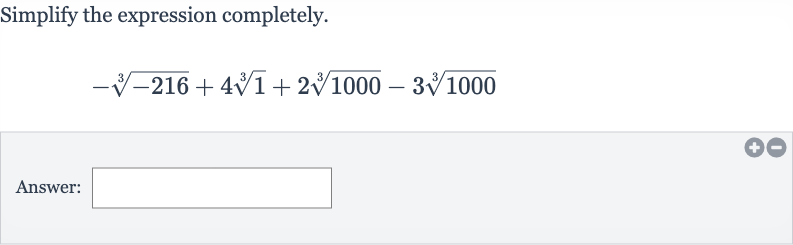
Q. Simplify the expression completely.Answer:
- Simplify cube root of : We will start by simplifying each term separately. The first term is the cube root of , which is because .
- Simplify cube root of : The second term is times the cube root of , which is simply because the cube root of is .
- Simplify cube root of : The third term is times the cube root of . The cube root of is because . So, times gives us .
- Simplify cube root of : The fourth term is times the cube root of , which we already found to be . So, times gives us .
- Combine simplified terms: Now, we combine all the simplified terms: .
- Add and subtract numbers: Adding and subtracting the numbers, we get , and .
- Final result: Finally, adding and , we get .