Full solution
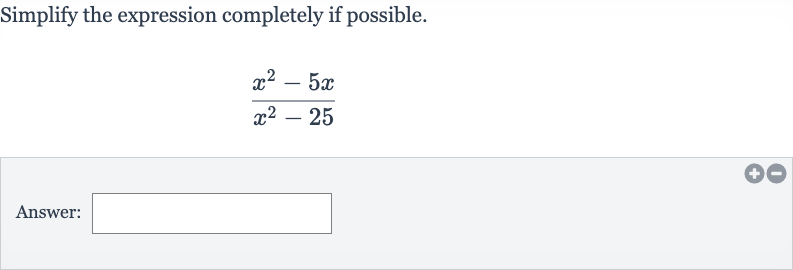
Q. Simplify the expression completely if possible.Answer:
- Factor Numerator and Denominator: Factor both the numerator and the denominator.The numerator can be factored by taking out the common factor , which gives us .The denominator is a difference of squares and can be factored into .So, the expression becomes:
- Cancel Common Factors: Cancel out the common factors.The factor is present in both the numerator and the denominator, so we can cancel it out.This gives us:
- Check for Further Simplification: Check for any further simplification.There are no common factors left, and we cannot simplify the expression any further.So, the simplified form of the expression is:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help