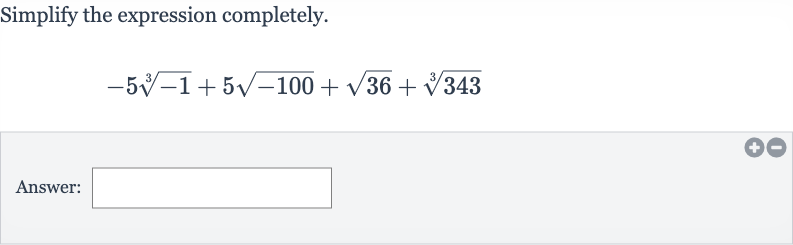
Simplify the expression completely. -5root(3)(-1)+5sqrt(-100)+sqrt36+root(3)(343) Answer:

Question

Simplify the expression completely.  -5root(3)(-1)+5sqrt(-100)+sqrt36+root(3)(343) Answer:

Bytelearn · Accepted Answer

Identify Terms: Identify the terms in the expression and simplify each term separately. -5root(3)(-1) involves the cube root of -1. 5sqrt(-100) involves the square root of -100, which is a complex number since the square root of a negative number is not real. sqrt(36) involves the square root of 36. root(3)(343) involves the cube root of 343.Simplify -5root(3)(-1): Simplify -5root(3)(-1). The cube root of -1 is -1, so -5 times the cube root of -1 is -5 times -1, which equals 5.Simplify 5sqrt(-100): Simplify 5sqrt(-100). The square root of -100 is not a real number; it is 10i, where i is the imaginary unit. So, 5 times the square root of -100 is 5 times 10i, which equals 50i.Simplify sqrt(36): Simplify sqrt(36). The square root of 36 is 6, since 6 times 6 equals 36.Simplify root(3)(343): Simplify root(3)(343). The cube root of 343 is 7, since 7 times 7 times 7 equals 343.Combine Simplified Terms: Combine the simplified terms. Add the real number terms 5 and 6, and keep the imaginary term 50i separate. The cube root of 343, which is 7, is also a real number and can be added to the other real numbers. 5 + 6 + 7 = 18Write Final Expression: Write the final simplified expression. The real part is 18, and the imaginary part is 50i. Since the original problem did not specify that we should only find the real-number root, we include the imaginary part in our answer. The final simplified expression is 18 + 50i.

Simplify the expression completely. $\newline$ $-5 \sqrt[3]{-1}+5 \sqrt{-100}+\sqrt{36}+\sqrt[3]{343}$ $\newline$ Answer:

Full solution

More problems from Roots of rational numbers

Related topics

Simplify the expression completely.\newline−5−13+5−100+36+3433 -5 \sqrt[3]{-1}+5 \sqrt{-100}+\sqrt{36}+\sqrt[3]{343} −53−1​+5−100​+36​+3343​\newlineAnswer:

Simplify the expression completely. $\newline$ $-5 \sqrt[3]{-1}+5 \sqrt{-100}+\sqrt{36}+\sqrt[3]{343}$ $\newline$ Answer: