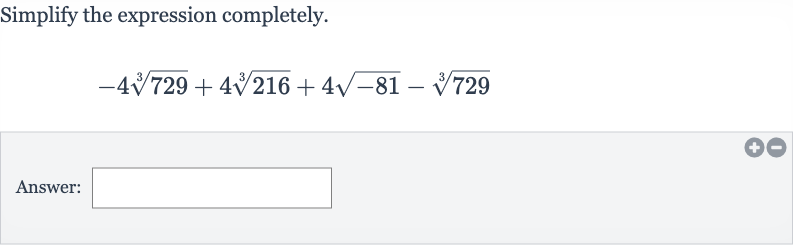
Simplify the expression completely. -4root(3)(729)+4root(3)(216)+4sqrt(-81)-root(3)(729) Answer:

Question

Simplify the expression completely.  -4root(3)(729)+4root(3)(216)+4sqrt(-81)-root(3)(729) Answer:

Bytelearn · Accepted Answer

Simplify Cube Roots: First, we will simplify each term separately, starting with the cube roots and then the square root of a negative number. -4root(3)(729) simplifies to -4 times the cube root of 729.Simplify Cube Roots: The cube root of 729 is 9 because 9^3 = 729. So, -4root(3)(729) simplifies to -4 * 9, which is -36.Simplify Cube Roots: Next, we simplify 4root(3)(216), which is 4 times the cube root of 216. The cube root of 216 is 6 because 6^3 = 216. So, 4root(3)(216) simplifies to 4 * 6, which is 24.Simplify Square Root: Now, we simplify 4sqrt(-81). The square root of -81 is not a real number; it is an imaginary number because you cannot take the square root of a negative number in the set of real numbers. So, 4sqrt(-81) is an imaginary number, 4i * 9, since the square root of 81 is 9.Combine Simplified Terms: Finally, we simplify -root(3)(729), which is the cube root of 729. As we found earlier, the cube root of 729 is 9. So, -root(3)(729) simplifies to -9.Combine Real and Imaginary Terms: Now, we combine all the simplified terms. -36 (from the first term) + 24 (from the second term) + 4i * 9 (from the third term) - 9 (from the fourth term).Final Simplified Expression: Combining the real number terms gives us -36 + 24 - 9, which simplifies to -21. The imaginary term remains 4i * 9, which is 36i.Since we cannot combine real numbers with imaginary numbers, the expression simplifies to -21 + 36i.

Simplify the expression completely. $\newline$ $-4 \sqrt[3]{729}+4 \sqrt[3]{216}+4 \sqrt{-81}-\sqrt[3]{729}$ $\newline$ Answer:

Full solution

More problems from Roots of rational numbers

Related topics

Simplify the expression completely.\newline−47293+42163+4−81−7293 -4 \sqrt[3]{729}+4 \sqrt[3]{216}+4 \sqrt{-81}-\sqrt[3]{729} −43729​+43216​+4−81​−3729​\newlineAnswer:

Simplify the expression completely. $\newline$ $-4 \sqrt[3]{729}+4 \sqrt[3]{216}+4 \sqrt{-81}-\sqrt[3]{729}$ $\newline$ Answer: