AI tutor
Full solution
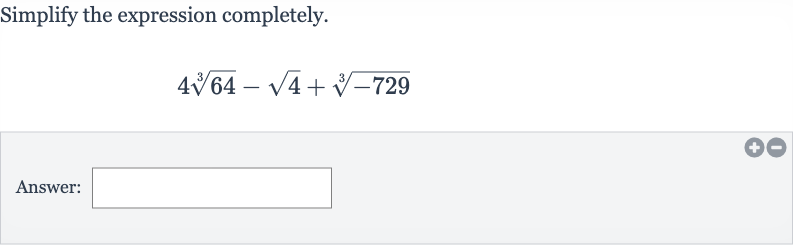
Q. Simplify the expression completely.Answer:
- Find Cube Root of : Simplify . The cube root of is , because . So, .
- Find Square Root of : Simplify .The square root of is , because .So, .
- Find Cube Root of : Simplify .The cube root of is , because .So, = .
- Combine Results: Combine the results from steps , , and .We have from step , from step (since we subtract the square root of ), and from step .Combine these values: .
- Perform Subtraction: Perform the subtraction. .