AI tutor
Full solution
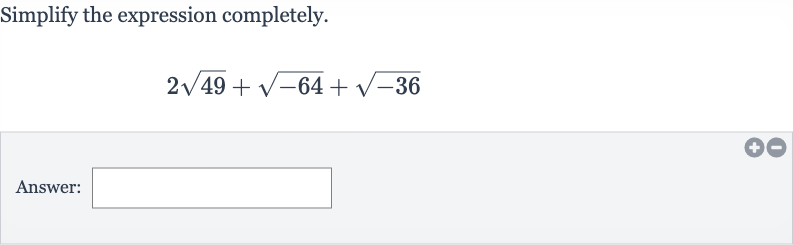
Q. Simplify the expression completely.Answer:
- Positive Number Simplification: Simplify the square root of a positive number.We have , which is times the square root of . The square root of is .So, .
- Negative Number Simplification: Simplify the square root of a negative number.We have , which involves the square root of a negative number. The square root of a negative number is an imaginary number. We can write as , which is , where is the imaginary unit.
- Another Negative Number Simplification: Simplify another square root of a negative number. Similarly, can be written as , which is .
- Combining Results: Combine the results from the previous steps.Now we combine the results from steps , , and . (from step ) + (from step ) + (from step ) = .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help