AI tutor
Full solution
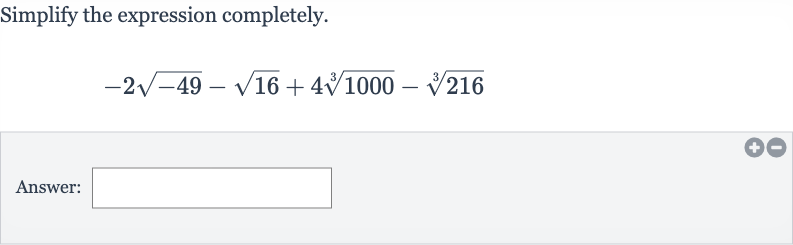
Q. Simplify the expression completely.Answer:
- Simplify : First, we will simplify each term in the expression separately. involves the square root of a negative number, which indicates the presence of an imaginary number.
- Simplify : The square root of is , where is the imaginary unit. Therefore, becomes , which simplifies to .
- Simplify : Next, we simplify . The square root of is , so simplifies to .
- Simplify : Now, we simplify . The cube root of is , because . Therefore, simplifies to , which is .
- Combine simplified terms: Finally, we simplify . The cube root of is , because . Therefore, simplifies to .
- Combine real numbers: Now we combine all the simplified terms: .
- Final simplified expression: Combining the real numbers gives us: , which simplifies to .
- Final simplified expression: Combining the real numbers gives us: , which simplifies to .The final simplified expression is , which includes a real part and an imaginary part.