AI tutor
Full solution
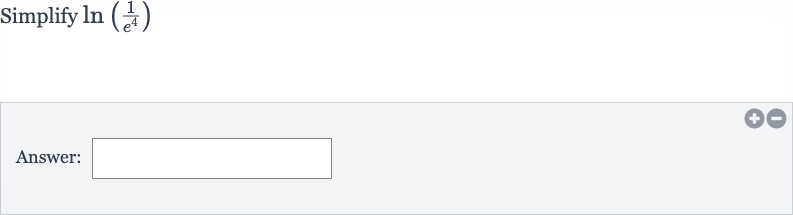
Q. Simplify Answer:
- Identify Components: Identify the components of the expression . In , we have a natural logarithm of a fraction where the denominator is raised to the power of .
- Apply Power Rule: Apply the logarithm power rule.The power rule of logarithms states that . We can apply this rule in reverse since the denominator is raised to the power of .
- Simplify Logarithms: Simplify the logarithms.We know that because . Also, because the base of the natural logarithm is .
- Perform Subtraction: Perform the subtraction.
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help