AI tutor
Full solution
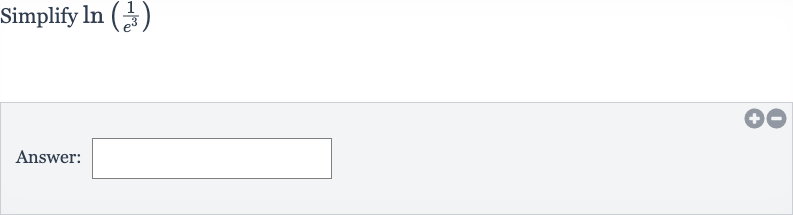
Q. Simplify Answer:
- Identify Components: Identify the components of the natural logarithm expression. Here, we have the natural logarithm of a fraction where the denominator is raised to the power of .
- Apply Power Rule: Apply the logarithm power rule.The power rule of logarithms states that . In this case, we can apply the rule in reverse to move the exponent on out in front of the logarithm.
- Simplify Logarithms: Simplify the logarithm of and the logarithm of to the power of .
is because .
is because , and using the power rule, .
So, - Calculate Final Result: Calculate the final result.
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help